
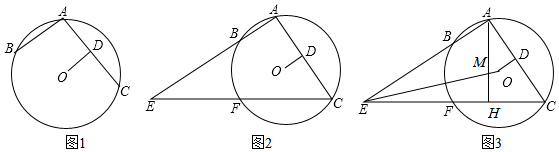
分析 (1)如图1,作辅助线,构建两个平行四边形,根据对角线互相垂直平分的四边形是菱形得:四边形AOCG是菱形,则AG=OC,再证明四边形ABOG是平行四边形,得:AB∥OG,可得结论;
(2)如图2,由弧相等,则所对的弦相等,由等边对等角得:∠FAC=∠FCA,由直角三角形两锐角互余可得结论;
(3)如图3,作辅助线,构建直角三角形,证明△FMN≌△FMH,得∠MFH=∠MFN,由直角三角形直角边和斜边的关系得:∠FAH=30°,依次求AH、AE、AC的长,最后在直角△ODC中,根据30°的正切得OD的长,从而求AB的长.
解答 证明:(1)如图1,延长OD到G,连接AG、GC、OC、AO、OB,
∵OD⊥AC,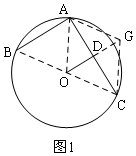
∴AD=DC,
∴四边形AOCG是菱形,
∴AG=OC,
∵OB=OC,
∴AG=OB,
∵AB=2OD,OG=2OD,
∴AB=OG,
∴四边形ABOG是平行四边形,
∴AB∥OG,
∵OG⊥AC,
∴AB⊥AC,
∴∠BAC=90°;
(2)如图2,连接AF,
∵$\widehat{AF}=\widehat{CF}$,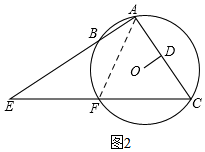
∴AF=CF,
∴∠FAC=∠FCA,
由(1)得:∠EAC=90°,
∴∠EAF+∠FAC=90°,
∠AEC+∠FCA=90°,
∴∠EAF=∠AEC,
∴AF=EF,
∴EF=CF;
(3)如图3,连接AF、BF、OA、OF、OC,过O作ON⊥EC于N,
则NF=NC,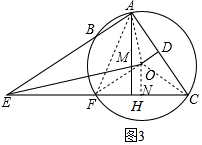
∵EF=FC,
∴EN=3FN,
∵AF=FC,OD⊥AC,OA=OC,
∴F、O、D三点共线,
∴∠OFN=∠AEC,
∴tan∠OFN=tan∠AEC=$\frac{AH}{EH}=\frac{ON}{FN}$,
∵tan∠OEN=$\frac{ON}{EN}$=$\frac{ON}{3FN}$,
∴AH=3MH,
即AM+MH=3MH,
AM=2MH,
∵AM=8,
∴MH=4,
∴AH=12,
∴CF=AF=$\sqrt{A{H}^{2}+F{H}^{2}}$=$\sqrt{1{2}^{2}+(\frac{7}{2})^{2}}$=$\frac{25}{2}$,
∴CH=$\frac{25}{2}$-$\frac{7}{2}$=9,AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
∵∠AOD=∠AFH,
∴tan∠AOD=tan∠AFH=$\frac{AD}{OD}$=$\frac{AH}{FH}$,
∴$\frac{\frac{15}{2}}{OD}=\frac{12}{\frac{7}{2}}$,
∴OD=$\frac{35}{16}$,
∴AB=2OD=$\frac{35}{8}$.
点评 本题是圆的综合题,考查了弦心距与弦的关系、圆心角与同弧所对的圆周角的关系、三角函数、直角三角形30°角的性质、等边三角形的性质和判定,难度适中,第3问,作出辅助线,证明∠FAH=30°是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 
| ||||||||||||||||||||||||||||||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
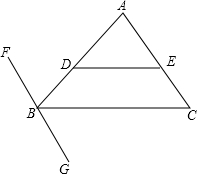 如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.
如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.
如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com