
【题目】如图,反比例函数y=![]() 与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=
与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=![]() .
.
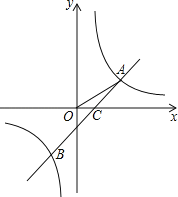
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值.
【答案】(1)y=![]() ,y=
,y=![]() x﹣1.(2)
x﹣1.(2)![]() .
.
【解析】
试题分析:(1)过点A作AE⊥x轴于点E,根据tanα=![]() 可得出m的值,进而得出反比例函数的解析式,根据B(﹣2,n)在反比例函数y=
可得出m的值,进而得出反比例函数的解析式,根据B(﹣2,n)在反比例函数y=![]() 的图象上得出B点坐标,再把A、B两点的坐标代入直线y=k2x+b即可得出其解析式;
的图象上得出B点坐标,再把A、B两点的坐标代入直线y=k2x+b即可得出其解析式;
(2)先求出C点坐标,再由A点坐标可得出AE的长,根据锐角三角函数的定义即可得出结论.
解:(1)过点A作AE⊥x轴于点E,
∵tan∠AOE=tanα=![]() ,
,
∴OE=4AE.
∵A(m,1),
∴AE=1,
∴OE=4,
∴A(4,1).
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k1=4,
∴反比例函数的解析式为y=![]() .
.
∵B(﹣2,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=2,
∴B(﹣2,﹣2).
将A、B两点的坐标代入直线y=k2x+b得,
 ,解得
,解得 ,
,
∴直线AB的解析式为y=![]() x﹣1.
x﹣1.
(2)∵直线AB的解析式为y=![]() x﹣1,令y=0,则x=2,
x﹣1,令y=0,则x=2,
∴C(2,0).
∵A(4,1),
∴CE=2,AE=1,
∴tanβ=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9
C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=10cm,sinA=![]() .如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)
.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)

(1)求AC,BC的长;
(2)当t为何值时,△APQ的面积为△ABC面积的![]() ;
;
(3)当t为何值时,△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,一边上的中线BD 将这个三角形的周长分为15和12两个部分,则该等腰三角形的底边长为 ( )
A.7 B.10 C.7或10 D.7或11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
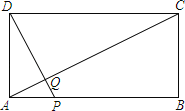
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
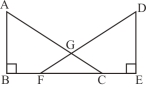
求证:(1)△ABC≌△DEF;
(2)GF=GC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
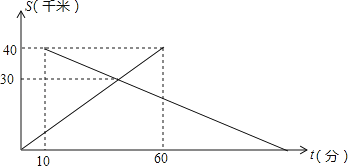
A.14:00 B.14:20 C.14:30 D.14:40
查看答案和解析>>
科目:初中数学 来源: 题型:
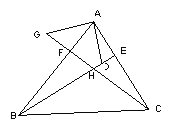
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com