
分析 (1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:an•am=an+m以及对数的含义,得出结论:logaM+logaN=logaMN.
解答 解:(1)∵22=4,24=16,26=64,
∴log24=2;log216=4;log264=6,
故答案为:2,4,6;
(2)由(1)知,∵2+4=6,
∴log24+log216=log264=log2(4×16),
故答案为:log24+log216=log264;
(3)设logaM=x,logaN=y,
则ax=M,ay=N,
∴MN=ax•ay=ax+y,
∴x+y=logaMN,即logaM+logaN=logaMN
故答案为:logaM+logaN=logaMN.
点评 此题主要考查了数字的变化规律.借考查对数,实际考查学生对指数的理解、掌握的程度;要求学生不但能灵活、准确的应用其运算法则,还要会类比、归纳,推测出对数应有的性质.


科目:初中数学 来源: 题型:解答题
 如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.
如图,一条抛物线经过(-2,5),(0,-3)和(1,-4)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
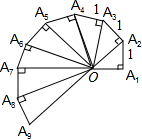 如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.
如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:判断题
( 6分) 已知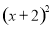 +
+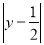 =0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为 ________________.
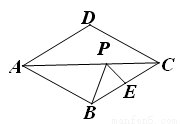
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<$\frac{4}{3}$ | B. | k<$\frac{4}{3}$且k≠0 | C. | k≤$\frac{4}{3}$ | D. | k≤$\frac{4}{3}$且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com