
分析 连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可.
解答 解: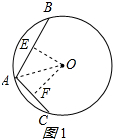 有两种情况:
有两种情况:
①如图1所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{2}}{2}$,
cos∠OAE=$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,∴∠BAC=30°+45°=75°;
②如图2所示:
连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE=$\frac{\sqrt{3}}{2}$,AF=CF=$\frac{\sqrt{2}}{2}$,
cos∠OAE═$\frac{AE}{OA}$=$\frac{\sqrt{3}}{2}$,cos∠OAF=$\frac{AF}{OA}$=$\frac{\sqrt{2}}{2}$,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=45°-30°=15°;
故答案为:75°或15°.
点评 本题考查了特殊角的三角函数值和垂径定理的应用.此题难度适中,解题的关键是根据题意作出图形,求出符合条件的所有情况.此题比较好,但是一道比较容易出错的题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{6{x}^{3}}$ | D. | $\sqrt{{x}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
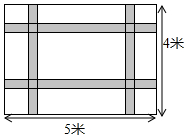 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com