练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，已知AB、AD是⊙O的弦，∠B=20°，∠D=15°，则∠BAD的度数是（　　）
    A．30°B．45°C．20°D．35°

    分析 连接OA，根据等腰三角形的性质求出∠DAO与∠BAO的度数，进而可得出结论．

    解答 解：连接OA，
    ∵OA=OD，OB=OA，
    ∴∠DAO=∠D=15°，∠BAO=∠B=20°，
    ∴∠BAD=∠DAO+∠BAO=15°+20°=35°．
    故选D．

    点评 本题考查的是圆周角定理，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

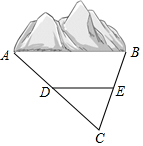    4．某地需要开辟一条笔直隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使C到A，B两点均可直接到达，测量找到AC和BC的中点D，E，测得DE的长为1 100m，则隧道AB的长度为（　　）
    A．3 300 mB．2 200 mC．1 100 mD．550 m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．【问题情境】如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
    【变式思考】如图2，四边形ABCD中，AB=5，BC=2，∠ABC=∠ACD=∠ADC=45°，求BD的长．
    【深入探究】如图3，在（2）的条件下，当△ACD在线段AC的左侧是，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的横坐标是（　　）
    A．2B．2n-1C．2nD．2n+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在“国际禁烟日”当天，某学习小组为了了解某社区6000个成年人中大约有多少人吸烟，随机抽查了200个成年人，结果其中有10个成年人吸烟，对于这个数据收集和处理问题，下列说法正确的是（　　）
    A．调查的方式是普查B．样本容量是200
    C．该小区只有190个成年人不吸烟D．该小区一定有300人吸烟

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．对点（x1，y1）和（x2，y2）定义两种新运算⊕和?，规定：
    （x1，y1）⊕（x2，y2）=（x1+x2，y1+y2），（x1，y1）?（x2，y2）=x1x2+y1y2，
    例如：（1，2）⊕（-2，3）=（1+（-2），2+3）=（-1，5）
    （1，2）?（-2，3）=1×（-2）+2×3=-2+6=4
    （1）试计算（-1，3）⊕（4，-2）=（3，1）
    （-1，3）?（4，-2）=-10
    （2）已知若（a，-1）⊕（4，b）=（5，-3），求a，b的值；
    （3）关于x的不等式（x，-1）?（4，x-1）≥p恰好有3个负整数解，求实数p的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列说法中正确的是（　　）
    A．最简分数的分子和分母都是素数
    B．两个素数一定互素
    C．数a的倒数是$\frac{1}{a}$
    D．如果两个数互为倒数，那么它们的积一定是1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若m＜0，mn＜0，则|n-m+1|-|m-n-5|的值是（　　）
    A．-4B．4C．2n-2m+4D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

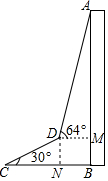    6．为了测量出大楼AB的高度，从距离楼底B处50米的点C（点C与楼底B在同一水平面上）出发，沿倾斜角为30°的斜坡CD前进20米到达点D，在点D处测得楼顶A的仰角为64°，求大楼AB的高度（结果精确到1米）（参考数据：sin64°≈0.9，cos64°≈0.4，tan64°≈2.1，$\sqrt{3}$≈1.7）

    查看答案和解析>>

    同步练习册答案