
”¾ĢāÄæ”æĀĢÉ«Ö²ĪļĻśŹŪ¹«Ė¾“ņĖćĻśŹŪÄ³Ę·ÖֵĔ°ÉĶŅ¶Ö²Īļ”±£¬ŌŚÕė¶ŌÕāÖÖ”°ÉĶŅ¶Ö²Īļ”±½ųŠŠŹŠ³”µ÷²éŗ󣬻ęÖĘĮĖŅŌĻĀĮ½ÕÅŗÆŹżĶ¼Ļó£®ĘäÖŠĶ¼¢ŁĪŖŅ»ĢõÖ±Ļߣ¬Ķ¼¢ŚĪŖŅ»ĢõÅ×ĪļĻߣ¬ĒŅÅ×ĪļĻ߶„µćĪŖ(6£¬1)£¬Ēėøł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
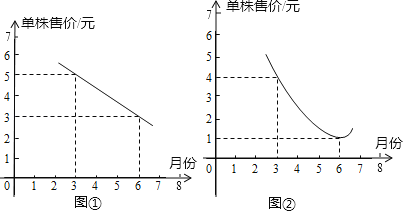
£Ø1£©Čē¹ū¹«Ė¾ŌŚ3ŌĀ·ŻĻśŹŪÕāÖÖ”°ÉĶŅ¶Ö²Īļ”±£¬µ„Öź»ńĄū¶ąÉŁŌŖ£»
£Ø2£©ĒėÖ±½ÓŠ“³öĶ¼Ļó¢ŁÖŠÖ±ĻߵĽāĪöŹ½£»
£Ø3£©ĒėÄćĒó³ö¹«Ė¾ŌŚÄÄøöŌĀĻśŹŪÕāÖÖ”°ÉĶŅ¶Ö²Īļ”±£¬µ„Öź»ńĄū×ī“ó£æ£Ø±ø×¢£ŗµ„Öź»ńĄū£½µ„ÖźŹŪ¼Ū©µ„Öź³É±¾£©
”¾“š°ø”æ£Ø1£©1£»£Ø2£©y1£½©![]() x+7£»£Ø3£©5ŌĀĻśŹŪÕāÖÖÖ²Īļ£¬µ„Öź»ńĄū×ī“ó
x+7£»£Ø3£©5ŌĀĻśŹŪÕāÖÖÖ²Īļ£¬µ„Öź»ńĄū×ī“ó
”¾½āĪö”æ
£Ø1£©“Ó×óĶ¼æ“£¬3ŌĀ·ŻŹŪ¼ŪĪŖ5ŌŖ£¬“ÓÓŅĶ¼æ“£¬3ŌĀ·ŻµÄ³É±¾ĪŖ4ŌŖ£¬ŌņĆæÖź»ńĄūĪŖ5©4£½1£ØŌŖ£©£¬¼“æÉĒó½ā£»
£Ø2£©µć£Ø3£¬5£©”¢£Ø6£¬3£©ĪŖŅ»“ĪŗÆŹżÉĻµÄµć£¬ĒóµĆÖ±Ļߵıķ“ļŹ½ĪŖ£ŗy1£½©![]() x+7£»
x+7£»
£Ø3£©ĒóµĆy2µÄ½āĪöŹ½ŗó¼ĘĖćy1©y2µÄÖµ£¬Åä·½æÉµĆ½įĀŪ£®
£Ø1£©“Ó×óĶ¼æ“£¬3ŌĀ·ŻŹŪ¼ŪĪŖ5ŌŖ£¬“ÓÓŅĶ¼æ“£¬3ŌĀ·ŻµÄ³É±¾ĪŖ4ŌŖ£¬ŌņĆæÖź»ńĄūĪŖ5©4£½1£ØŌŖ£©£¬
¹Ź“š°øĪŖ£ŗ1£»
£Ø2£©ÉčÖ±Ļߵıķ“ļŹ½ĪŖ£ŗy1£½kx+b£Øk”Ł0£©£¬
°Ńµć£Ø3£¬5£©”¢£Ø6£¬3£©“śČėÉĻŹ½µĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ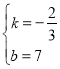 £¬
£¬
”ąÖ±Ļߵıķ“ļŹ½ĪŖ£ŗy1£½©![]() x+7£»
x+7£»
£Ø3£©Éč£ŗÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗy2£½a£Øx©m£©2+n£¬
”߶„µćĪŖ£Ø6£¬1£©£¬ŌņŗÆŹż±ķ“ļŹ½ĪŖ£ŗy2£½a£Øx©6£©2+1£¬
°Ńµć£Ø3£¬4£©“śČėÉĻŹ½µĆ£ŗ
4£½a£Ø3©6£©2+1£¬½āµĆ£ŗa£½![]() £¬
£¬
ŌņÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗy2£½![]() £Øx©6£©2+1£¬
£Øx©6£©2+1£¬
¹Ź“š°øĪŖ£ŗy1£½©![]() x+7£»y2£½
x+7£»y2£½![]() £Øx©6£©2+1£¬
£Øx©6£©2+1£¬
£Ø3£©y1©y2£½©![]() x+7©
x+7©![]() £Øx©6£©2©1£½©
£Øx©6£©2©1£½©![]() £Øx©5£©2+
£Øx©5£©2+![]() £¬
£¬
”ßa£½©![]() £¼0£¬
£¼0£¬
”ąx£½5Ź±£¬ŗÆŹżČ”µĆ×ī“óÖµ£¬
¹Ź£ŗ5ŌĀĻśŹŪÕāÖÖÖ²Īļ£¬µ„Öź»ńĄū×ī“ó£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
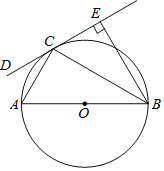
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬CDĒŠ”ŃOÓŚµćC£¬BE”ĶCDÓŚE£¬Į¬½ÓAC£¬BC£®
£Ø1£©ĒóÖ¤£ŗBCĘ½·Ö”ĻABE£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ3£¬cosA£½![]() £¬ĒóCEµÄ³¤£®
£¬ĒóCEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
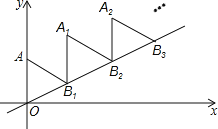
”¾ĢāÄæ”æČēĶ¼£¬·ÅÖƵĔ÷OAB1£¬”÷B1A1B2£¬”÷B2A2B3£¬¶¼ŹĒ±ß³¤ĪŖ2µÄµČ±ßČż½ĒŠĪ£¬±ßAOŌŚYÖįÉĻ£¬µćB1”¢B2”¢B3¶¼ŌŚÖ±Ļßy=![]() xÉĻ£¬ŌņµćA2019µÄ×ų±źĪŖ__________________
xÉĻ£¬ŌņµćA2019µÄ×ų±źĪŖ__________________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§æŖÉčµÄĢåӿєŠŽæĪÓŠĄŗĒņ”¢×ćĒņ”¢ÅÅĒņ”¢ÓšĆ«Ēņ”¢Ę¹ÅŅĒņ£¬Ń§ÉśæÉŅŌøł¾Ż×Ō¼ŗµÄ°®ŗĆŃ”ŠŽĘäÖŠ1ĆÅ.ij°ą°ąÖ÷ČĪ¶ŌČ«°ąĶ¬Ń§µÄŃ”æĪĒéæö½ųŠŠĮĖµ÷²éĶ³¼Ę£¬ÖĘ³ÉĮĖĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼(Ķ¼(1)ŗĶĶ¼(2))£ŗ
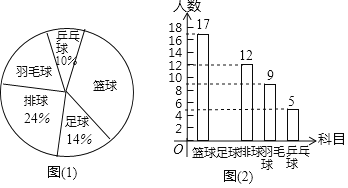
(1)ĒėÄćĒó³öøĆ°ąµÄ×ÜČĖŹż£¬²¢²¹Č«ĢõŠĪĶ¼(×¢£ŗŌŚĖł²¹Š”¾ŲŠĪÉĻ·½±ź³öČĖŹż)£»
(2)ŌŚøĆ°ąĶÅÖ§²æ4ČĖÖŠ£¬ÓŠ1ČĖŃ”ŠŽÅÅĒņ£¬2ČĖŃ”ŠŽÓšĆ«Ēņ£¬1ČĖŃ”ŠŽĘ¹ÅŅĒņ.Čē¹ūøĆ°ą°ąÖ÷ČĪŅŖ“ÓĖūĆĒ4ČĖÖŠČĪŃ”2ČĖ×÷ĪŖѧɜ»įŗņŃ”ČĖ£¬ÄĒĆ“Ń”³öµÄĮ½ČĖÖŠĒ”ŗĆÓŠ1ČĖŃ”ŠŽÅÅĒņ”¢1ČĖŃ”ŠŽÓšĆ«ĒņµÄøÅĀŹŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¼ÖŠµÄĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¾łĪŖ1£¬ĆæøöŠ”Õż·½ŠĪµÄ¶„µć½Š×öøńµć£®Ļ߶Ī![]() ŗĶ
ŗĶ![]() µÄ¶Ėµć
µÄ¶Ėµć![]() ¾łŌŚøńµćÉĻ£®
¾łŌŚøńµćÉĻ£®
£Ø1£©ŌŚĶ¼ÖŠ»³öŅŌ![]() ĪŖŅ»±ßµÄ
ĪŖŅ»±ßµÄ![]() £¬µć
£¬µć![]() ŌŚøńµćÉĻ£¬Ź¹
ŌŚøńµćÉĻ£¬Ź¹![]() µÄĆ껿ĪŖ4£¬ĒŅ
µÄĆ껿ĪŖ4£¬ĒŅ![]() µÄŅ»øö½ĒµÄÕżĒŠÖµŹĒ
µÄŅ»øö½ĒµÄÕżĒŠÖµŹĒ![]() £»
£»
£Ø2£©ŌŚĶ¼ÖŠ»³öŅŌ![]() ĪŖ¶„½ĒµÄµČŃü
ĪŖ¶„½ĒµÄµČŃü![]() £Ø·ĒÖ±½ĒČż½ĒŠĪ£©£¬µć
£Ø·ĒÖ±½ĒČż½ĒŠĪ£©£¬µć![]() ŌŚøńµćÉĻ£®ĒėÄćÖ±½ÓŠ“³ö
ŌŚøńµćÉĻ£®ĒėÄćÖ±½ÓŠ“³ö![]() µÄĆ껿£®
µÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪABCDÖŠ£¬AB£½5£¬Į¬½ÓBD£¬sin”ĻABD£½![]() £¬µćPŹĒÉäĻßBCÉĻŅ»µć£Ø²»ÓėµćBÖŲŗĻ£©£¬APÓė¶Ō½ĒĻßBD½»ÓŚµćE£¬Į¬½ÓEC£®
£¬µćPŹĒÉäĻßBCÉĻŅ»µć£Ø²»ÓėµćBÖŲŗĻ£©£¬APÓė¶Ō½ĒĻßBD½»ÓŚµćE£¬Į¬½ÓEC£®
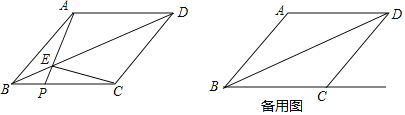
£Ø1£©ĒóÖ¤£ŗAE£½CE£»
£Ø2£©µ±µćPŌŚĻ߶ĪBCÉĻŹ±£¬ÉčBP£½n£Ø0£¼n£¼5£©£¬Ēó”÷PECµÄĆ껿£»£ØÓĆŗ¬nµÄ“śŹżŹ½±ķŹ¾£©
£Ø3£©µ±µćPŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±£¬Čō”÷PECŹĒÖ±½ĒČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³öBPµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ±ĻŅµµäĄńµÄæŖÄ»Ź½ÉĻŠčŅŖ²É¹ŗ»ØµźµÄĻŹ»Ø£®»ØµźĢį¹©¼×”¢ŅŅĮ½ÖÖŌģŠĶµÄ»ØŹųŹżĮæČōøÉ£¬¼×ÖÖ»ØŹųÓÉ4Ö¦ŗģ»Ø”¢1Ö¦»Ę»ØŗĶ1Ö¦×Ļ»Ø“īÅä¶ų³É£¬ŅŅÖÖ»ØŹųÓÉ4Ö¦»Ę»ØŗĶ2Ö¦×Ļ»Ø“īÅä¶ų³É£®ŅŃÖŖĆæÖ¦ŗģ»Ø”¢»Ę»ØŗĶ×Ļ»ØµÄ³É±¾Ö®±ČŹĒ3:2:1£¬¼×”¢ŅŅĮ½ÖÖŌģŠĶµÄ»ØŹųŹżĮæÖ®±ČŹĒ2£ŗ9£®¼×”¢ŅŅĮ½ÖÖ»ØŹų³É±¾¼Ū·Ö±šĪŖĆæÖÖŌģŠĶµÄČżÖÖĻŹ»ØµÄ³É±¾Ö®ŗĶ£¬¼×ÖÖ»ØŹųµÄĻśŹŪĄūČóĀŹŹĒ20%£¬ŅŅÖÖ»ØŹųµÄĻśŹŪĄūČóĀŹĪŖ10%£¬Õā“ĪĀņĀō£¬»Øµź»ńµĆµÄĄūČóĀŹŹĒ___________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£æŖÕ¹ĮĖ”°»„Öś”¢Ę½µČ”¢øŠ¶÷”¢ŗĶŠ³”¢½ųČ””±Ö÷Ģā°ą»į»ī¶Æ£¬»ī¶Æŗ󣬾Ķ»ī¶ÆµÄ![]() øöÖ÷Ģā½ųŠŠĮĖ³éŃłµ÷²é£ØĆæĪ»Ķ¬Ń§Ö»Ń”×ī¹Ų×¢µÄŅ»øö£©£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®øł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
øöÖ÷Ģā½ųŠŠĮĖ³éŃłµ÷²é£ØĆæĪ»Ķ¬Ń§Ö»Ń”×ī¹Ų×¢µÄŅ»øö£©£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®øł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Õā“Īµ÷²éµÄѧɜ¹²ÓŠ¶ąÉŁĆū£æ
£Ø2£©Ēė½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£¬²¢ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ¼ĘĖć³ö”°½ųČ””±Ėł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£®
£Ø3£©Čē¹ūŅŖŌŚÕā![]() øöÖ÷ĢāÖŠČĪŃ”Į½øö½ųŠŠµ÷²é£¬øł¾Ż£Ø2£©ÖŠµ÷²é½į¹ū£¬ÓĆŹ÷דĶ¼»ņĮŠ±ķ·Ø£¬ĒóĒ”ŗĆŃ”µ½Ń§Éś¹Ų×¢×ī¶ąµÄĮ½øöÖ÷ĢāµÄøÅĀŹ£Ø½«»„Öś”¢Ę½µČ”¢øŠ¶÷”¢ŗĶŠ³”¢½ųČ”ŅĄ“Ī¼ĒĪŖA”¢B”¢C”¢D”¢E£©£®
øöÖ÷ĢāÖŠČĪŃ”Į½øö½ųŠŠµ÷²é£¬øł¾Ż£Ø2£©ÖŠµ÷²é½į¹ū£¬ÓĆŹ÷דĶ¼»ņĮŠ±ķ·Ø£¬ĒóĒ”ŗĆŃ”µ½Ń§Éś¹Ų×¢×ī¶ąµÄĮ½øöÖ÷ĢāµÄøÅĀŹ£Ø½«»„Öś”¢Ę½µČ”¢øŠ¶÷”¢ŗĶŠ³”¢½ųČ”ŅĄ“Ī¼ĒĪŖA”¢B”¢C”¢D”¢E£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬¶Ō³ĘÖįĪŖx=1£¬¾¹żµć£Ø-1£¬0£©£¬ÓŠĻĀĮŠ½įĀŪ£ŗ¢Łabc£¼0£»¢Śa+c£¾b£»¢Ū3a+c=0£»¢Üa+b£¾m£Øam+b£©£ØĘäÖŠm”Ł1£©ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø””””£©
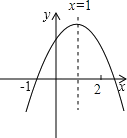
A. 1øö
B. 2øö
C. 3øö
D. 4øö
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com