
【题目】已知抛物线y=a(x﹣1)2﹣3(a≠0)的图象与y轴交于点A(0,﹣2),顶点为B.
(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值;
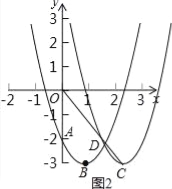
(4)若将抛物线平移m(m≠0)个单位,所得新抛物线的顶点记作C,与原抛物线的交点记作D,问:点O、C、D能否在同一条直线上?若能,请求出m的值;若不能,请说明理由.
【答案】(1)a=1,B(1,-3);(2)y=-x-2;(3)P(![]() ,0);(4)能,m=2或-3.
,0);(4)能,m=2或-3.
【解析】
试题分析:(1)把A点坐标代入解析式中可求得a值,根据顶点式可写出B点坐标;(2)由(1)可知A、B坐标,直线AB解析式可求出;(3)找出A点关于x轴对称点E,连接BE交x轴于点P.求出BE解析式即可求出点P坐标;(4)如图2,设抛物线向右平移m(若m>0表示向右平移,若m<0表示向左平移)个单位,得到新的抛物线的顶点C(1+m,﹣3),可求出直线OC解析式,解新旧抛物线联立方程组求得交点D坐标为(![]() ,
,![]() ),把D坐标代到OC解析式中得到m=2或m=﹣3,即可得到结论.
),把D坐标代到OC解析式中得到m=2或m=﹣3,即可得到结论.
试题解析:(1)把A(0,﹣2)代入y=a(x﹣1)2﹣3得﹣2=a(0﹣1)2﹣3,解得:a=1,∴y=(x﹣1)2﹣3,∴B(1,﹣3);(2)设一次函数的解析式为y=kx+b,将A、B两点的坐标代入得:![]() ,
,
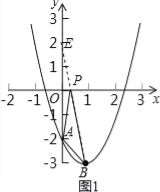
解得![]() ,∴一次函数的解析式为y=﹣x﹣2;(3)A点关于x轴的对称点记作E,则E(0,2),
,∴一次函数的解析式为y=﹣x﹣2;(3)A点关于x轴的对称点记作E,则E(0,2),
如图1,连接EB交x轴于点P,则P点即为所求,设直线BE的解析式为y=px+q,则![]() ,解得
,解得![]() ,∴直线BE:y=﹣5x+2,当y=0时,0=-5x+2,解得x=-
,∴直线BE:y=﹣5x+2,当y=0时,0=-5x+2,解得x=-![]() .∴P(
.∴P(![]() ,0);(4)如图2,设抛物线向右平移m(若m>0表示向右平移,若m<0表示向左平移)个单位,则所得新的抛物线的顶点C(1+m,﹣3),∴直线OC的解析式为
,0);(4)如图2,设抛物线向右平移m(若m>0表示向右平移,若m<0表示向左平移)个单位,则所得新的抛物线的顶点C(1+m,﹣3),∴直线OC的解析式为![]() ,∴新抛物线解析式为 y=(x﹣1﹣m)2﹣3,解
,∴新抛物线解析式为 y=(x﹣1﹣m)2﹣3,解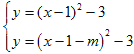 ,得
,得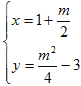 ,∴两抛物线的交点D(
,∴两抛物线的交点D(![]() ,
,![]() ),代入直线OC解析式中得
),代入直线OC解析式中得![]() ,解得:m=2或m=﹣3,∴O、C、D三点能够在同一直线上,
,解得:m=2或m=﹣3,∴O、C、D三点能够在同一直线上,
此时m=2或m=﹣3.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
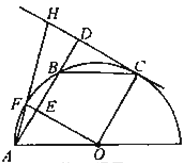
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF的长和半径OA的长.
,求EF的长和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一个n边形的某个顶点出发,分别连接这个点与其他顶点可以把这个n边形分割成三角形个数是( )
A.3个
B.(n﹣1)个
C.5个
D.(n﹣2)个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线m外有一定点A,A到直线m的距离是7 cm,B是直线m上的任意一点,则线段AB的长度:AB___________7 cm.(填写“<”“>”“=”“≤”或“≥”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com