练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

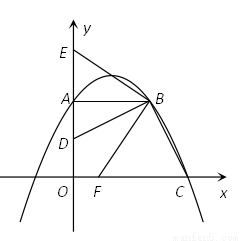
    如图，已知直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝AB＝2，OC＝3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于E和F．

    （1）求经过A、B、C三点的抛物线的解析式；

    （2）当BE经过（1）中抛物线的顶点时，求CF的长；

    （3）连结EF，设△BEF与△BFC的面积之差为S，问：当CF为何值时S最小，并求出这个最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届江苏省九年级下学期第一次学情调研数学试卷（解析版） 题型：单选题

    运用乘法公式计算的结果是

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年山东省文慧学校八年级下学期第一次月考数学试卷（解析版） 题型：填空题

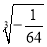    的相反数是______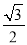， －1的绝对值是 ______________

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．某种正方形合金板材的成本y（元）与它的面积成正比．设它的边长为x厘米，当x=2时，y=16，那么当成本为72元时，边长为（　　）
    A．4厘米B．3$\sqrt{2}$厘米C．2$\sqrt{3}$厘米D．6厘米

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

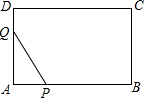    8．如图，矩形ABCD中，AB=2AD=4cm，动点P从点A出发，以lcm/s的速度沿线段AB向点B运动，动点Q同时从点A出发，以2cm/s的速度沿折线AD→DC→CB向点B运动，当一个点停止时另一个点也随之停止．设点P的运动时间是x（S）时，△APQ的面积是y（cm2），则能够反映y与x之间函数关系的图象大致是（　　）
    A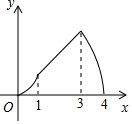．B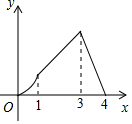．C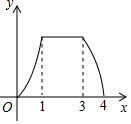．D．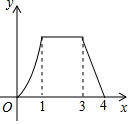

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

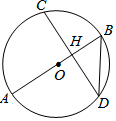    17．如图，AB是⊙O的直径，点B是弧CD的中点，AB交弦CD于点H，且CD=2$\sqrt{3}$，BD=2，则AB的长为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

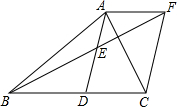    4．在△ABC中，点D在BC边上，点E是线段AD的中点，过点A作BC的平行线与BE的延长线于点F，连结CF，若AF=DC．
    （1）求证：BD=DC；
    （2）当四边形ADCF为正方形时，线段AB与BC有何数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

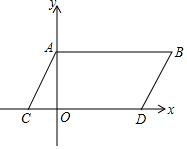    1．如图，在平面直角坐标系中，点A，B坐标分别为A（0，a），B（b，a），且实数a，b满足（a-3）2+|b-5|=0，现同时将点A，B分别向下平移3个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．
    （1）求点C，D的坐标及四边形ABDC的面积；
    （2）在y轴上是否存在一点M，连接MC，MD，使S△MCD=S四边形ABDC？若存在这样一点，求出点M的坐标；若不存在，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．问题再现：
    数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
    例如：利用图形的几何意义证明完全平方公式．
    证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
    这个图形的面积可以表示成：
    （a+b）2或　a2+2ab+b2
    ∴（a+b）2 =a2+2ab+b2
    这就验证了两数和的完全平方公式．
    类比解决：
    （1）请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
    问题提出：如何利用图形几何意义的方法证明：13+23=32？
    如图2，A表示1个1×1的正方形，即：1×1×1=13
    B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23
    而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
    由此可得：13+23=（1+2）2=32
    尝试解决：
    （2）请你类比上述推导过程，利用图形的几何意义确定：13+23+33=62．（要求写出结论并构造图形写出推证过程）．
    （3）问题拓广：
    请用上面的表示几何图形面积的方法探究：13+23+33+…+n3=[$\frac{1}{2}$n（n+1）]2．（直接写出结论即可，不必写出解题过程）

    查看答案和解析>>

    同步练习册答案