练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

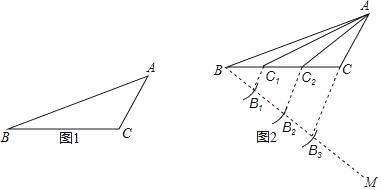
    【题目】石景山区八角北路有一块三角形空地（如图1）准备绿化，拟从点A出发，将△ABC分成面积相等的三个三角形，栽种三种不同的花草．

    下面是小美的设计（如图2）．

    作法：（1）作射线BM；

    （2）在射线BM上顺次截取BB1=B1B2=B2B3；

    （3）连接B3C，分别过B1、B2作B1C1∥B2C2∥B3C，交BC于点C1、C2；

    （4）连接AC1、AC2．则．

    请回答，成立的理由是：

    ①_____；

    ②_____．

    【答案】平行线分线段成比例定理； 等底共高．

    【解析】

    根据平行线分线段成比例定理和等底共高求解可得．

    解：由BB1=B1B2=B2B3且B1C1∥B2C2∥B3C，依据平行线分线段成比例定理知BC1=C1C2=C2C，

    再由△ABC1，△AC1C2与△AC2C等底共高知，

    故答案为：①平行线分线段成比例定理；

    ②等底共高．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，对称轴为直线的抛物线与x轴相交于A、B两点，其中A点的坐标为（－3，0）。

    （1）求点B的坐标；

    （2）已知，C为抛物线与y轴的交点。

    ①若点P在抛物线上，且，求点P的坐标；

    ②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，∠B＝30°，O是BC上一点，以点O为圆心，OB长为半径作圆，恰好经过点A，并与BC交于点D．

    （1）求证：CA是⊙O的切线．

    （2）若AB＝2，求图中阴影部分的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，函数y1=－x+4的图象与函数y2= (x＞0)的图象交于 A(a，1)、B(1，b)两点.

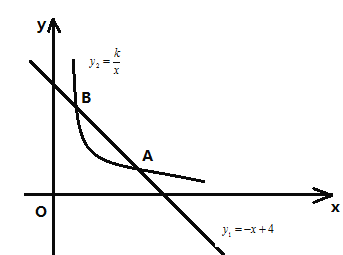
    (1)求a，b及y2的函数关系式；

    (2)观察图象，当x＞0时，比较y1与y2大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

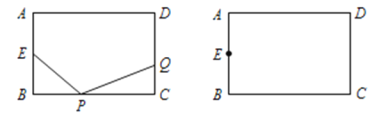
    【题目】已知：如图，在长方形中，AB=4cm，BC=6cm，点为中点，如果点在线段上以每秒2cm的速度由点向点运动，同时，点在线段上由点向点运动．设点运动时间为秒，若某一时刻△BPE与△CQP全等，求此时的值及点的运动速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

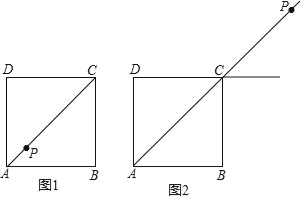
    【题目】在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．

    （1）当点P在线段AC上时，如图1．

    ①依题意补全图1；

    ②若EQ=BP，则∠PBE的度数为　 　，并证明；

    （2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】河南省旅游资源丰富，2013～2017年旅游收入不断增长，同比增速分别为：15.3%，12.7%，15.3%，14.5%，17.1%．关于这组数据，下列说法正确的是（　　）

    A. 中位数是12.7% B. 众数是15.3%

    C. 平均数是15.98% D. 方差是0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD是BC边上的中线，AE是BC边上的高．

    （1）若∠ACB＝100°，求∠CAE的度数；

    （2）若S△ABC＝12，CD＝4，求高AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，已知AD是角平分线，∠B＝66°，∠C＝54°.

    (1)求∠ADB的度数；

    (2)若DE⊥AC于点E，求∠ADE的度数．

    查看答案和解析>>

    同步练习册答案