
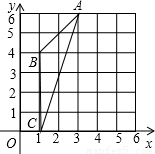
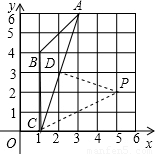
 解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)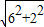 =2
=2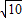 ,(2分)
,(2分) =2
=2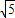 ,(3分)
,(3分)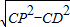 =
=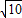 ,(4分)
,(4分)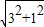 =
=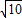 .(4分)
.(4分)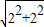 =
=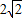 ,ι大=
,ι大= =
=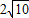 ,(7分)
,(7分)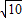 +
+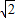 )π. (9分)
)π. (9分)

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《锐角三角函数》(05)(解析版) 题型:解答题
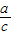 ,cosA=
,cosA=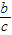 ,tanA=
,tanA=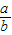 .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.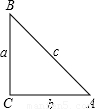
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《圆》(10)(解析版) 题型:解答题
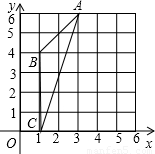
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《三角形》(14)(解析版) 题型:解答题
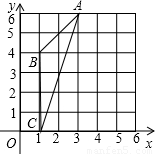
查看答案和解析>>
科目:初中数学 来源:2008年甘肃省庆阳市中考数学试卷(解析版) 题型:解答题
 ,cosA=
,cosA= ,tanA=
,tanA= .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com