
【题目】在Rt△ABC中,∠ACB=90°,AC=1,记∠ABC=α,点D为射线BC上的动点,连接AD,将射线DA绕点D顺时针旋转α角后得到射线DE,过点A作AD的垂线,与射线DE交于点P,点B关于点D的对称点为Q,连接PQ.
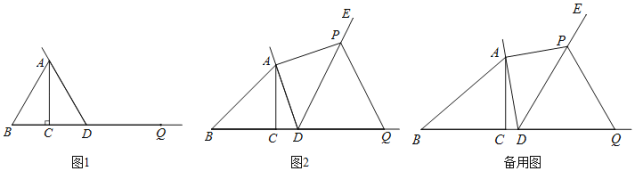
(1)当△ABD为等边三角形时,
①依题意补全图1;
②PQ的长为 ;
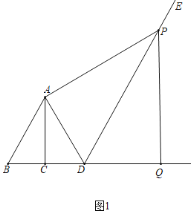
(2)如图2,当α=45°,且BD=![]() 时,求证:PD=PQ;
时,求证:PD=PQ;
(3)设BC=t,当PD=PQ时,直接写出BD的长.(用含t的代数式表示)
【答案】(1)①详见解析;②2;(2)详见解析;(3)BD=![]() .
.
【解析】
(1)①根据题意画出图形即可.
②解直角三角形求出PA,再利用全等三角形的性质证明PQ=PA即可.
(2)作PF⊥BQ于F,AH⊥PF于H.通过计算证明DF=FQ即可解决问题.
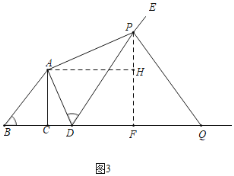
(3)如图3中,作PF⊥BQ于F,AH⊥PF于H.设BD=x,则CD=x﹣t, ![]() ,利用相似三角形的性质构建方程求解即可解决问题.
,利用相似三角形的性质构建方程求解即可解决问题.
(1)解:①补全图形如图所示:
②∵△ABD是等边三角形,AC⊥BD,AC=1
∴∠ADC=60°,∠ACD=90°
∴![]()
∵∠ADP=∠ADB=60°,∠PAD=90°
∴PA=ADtan60°=2
∵∠ADP=∠PDQ=60°,DP=DP.DA=DB=DQ
∴△PDA≌△PDQ(SAS)
∴PQ=PA=2.
(2)作PF⊥BQ于F,AH⊥PF于H,如图:
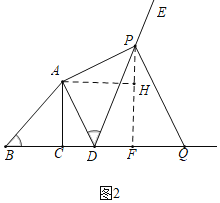
∵PA⊥AD,
∴∠PAD=90°
由题意可知∠ADP=45°
∴∠APD=90°﹣45°=45°=∠ADP
∴PA=PD
∵∠ACB=90°
∴∠ACD=90°
∵AH⊥PF,PF⊥BQ
∴∠AHF=∠HFC=∠ACF=90°
∴四边形ACFH是矩形
∴∠CAH=90°,AH=CF
∵∠ACH=∠DAP=90°
∴∠CAD=∠PAH
又∵∠ACD=∠AHP=90°
∴△ACD≌△AHP(AAS)
∴AH=AC=1
∴CF=AH=1
∵![]() ,BC=1,B,Q关于点D对称
,BC=1,B,Q关于点D对称
∴![]() ,
,![]()
∴![]()
∴F为DQ中点
∴PF垂直平分DQ
∴PQ=PD.
(3)如图3中,作PF⊥BQ于F,AH⊥PF于H.设BD=x,则CD=x﹣t,![]()
∵PD=PQ,PF⊥DQ
∴![]()
∵四边形AHFC是矩形
∴![]()
∵△ACB∽△PAD
∴![]()
∴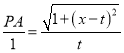
∴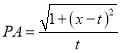
∵△PAH∽△DAC
∴![]()
∴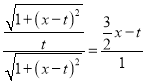
解得![]()
∴![]() .
.
故答案是:(1)①详见解析;②2;(2)详见解析;(3)![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月22日14时30分,全球新冠肺炎确诊病例达305740例,超过30万,死亡病例累计12762人,将“305740”这个数字用科学记数法表示保留两位有效数字为( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半圆O中,AB为直径,AC、AD为两条弦,且∠CAD+∠CAB=90°.
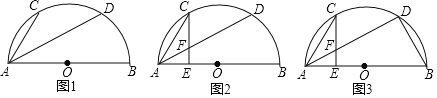
(1)如图1,求证:弧AC等于弧CD;
(2)如图2,点E在直径AB上,CE交AD于点F,若AF=CF,求证:AD=2CE;
(3)如图3,在(2)的条件下,连接BD,若AE=4,BD=12,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
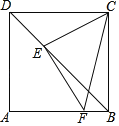
【题目】如图,在正方形ABCD中,AB=6,点E在对角线BD上,DE=2![]() ,连接CE,过点E作EF⊥CE,交线段AB于点F
,连接CE,过点E作EF⊥CE,交线段AB于点F
(1)求证:CE=EF;
(2)求FB的长;
(3)连接FC交BD于点G.求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了了解当年春游时学生的个人消费情况,从其中一所学校的初三年级中随机抽取了部分学生春游消费情况进行调查,并将这部分学生的消费额绘制成频率分布直方图.已知从左至右第一组的人数为12名.请根据所给的信息回答:

(1)被抽取调查的学生人数为 名;
(2)从左至右第五组的频率是 ;
(3)假设每组的平均消费额以该组的最小值计算,那么被抽取学生春游的最低平均消费额为 元;
(4)以第(3)小题所求得的最低平均消费额来估计该地区全体学生春游的最低平均消费额,你认为是否合理?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
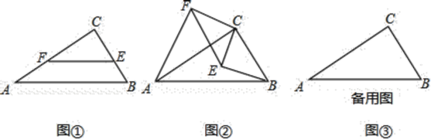
【题目】![]() 尝试探究:如图
尝试探究:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,E,F分别是BC,AC上的点,且
,E,F分别是BC,AC上的点,且![]() ,则
,则![]() ______;
______;
![]() 类比延伸:如图
类比延伸:如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点C顺时针旋转,则在旋转的过程中,
绕点C顺时针旋转,则在旋转的过程中,![]() 值是否发生变化?请仅就图
值是否发生变化?请仅就图![]() 的情形写出推理过程;
的情形写出推理过程;
![]() 拓展运用:若
拓展运用:若![]() ,
,![]() ,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y![]() 的图象经过点P(3,4).
的图象经过点P(3,4).
(1)求k的值;
(2)求OP的长;
(3)直线y=mx(m≠0)与反比例函数的图象有两个交点A,B,若AB>10,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
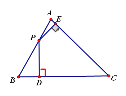
【题目】如图,在△ABC中,∠C=45°,∠B=60°,BC为![]() +1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com