
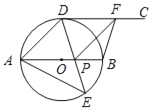
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE= 时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE= 时,四边形BFDP是正方形.
【答案】(1)详见解析;(2)①67.5°;②90°.
【解析】
(1)连接OD,由切线的性质得到∠ODF=90°,再由已知得到∠AOD=2∠AED=90°,从而得到∠ODF=∠AOD,进而证明CD∥AB;
(2)①根据菱形的性质进行角度运算即可得出;
②根据正方形的性质运算角度即可得出.
解:(1)如图,连接OD,
∵射线DC切⊙O于点D,
∴OD⊥CD,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,即∠ODF=∠AOD,
∴CD∥AB.

(2)①连接AF与DP交于点G,如图所示,
∵四边形ADFP是菱形,∠AED=45°,OA=OD,
∴AF⊥DP,∠AOD=90°,∠DAG=∠PAG,
∴∠AGE=90°,∠DAO=45°,
∴∠EAG=45°,∠DAG=∠PAG=22.5°,
∴∠EAD=∠DAG+∠EAG=22.5°+45°=67.5°,
故答案为:67.5°;
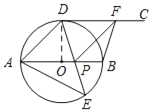
②∵四边形BFDP是正方形,
∴BF=FD=DP=PB,
∠DPB=∠PBF=∠BFD=∠FDP=90°,
∴此时点P与点O重合,
∴此时DE是直径,
∴∠EAD=90°,
故答案为:90°.


科目:初中数学 来源: 题型:
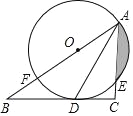
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店要运一批货物,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完这批货物,则乙车所运趟数是甲车的2倍;已知乙车毎趟运费比甲车少200元.
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此批货物,需运多少趟;
(3)若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此批货物,其中x、y均为正整数,设总运费为w(元),求w与x的函数关系式,直接写出w的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a﹣b|=3,|b﹣c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
![]()
A. 在A的左边 B. 介于A、B之间 C. 介于B、C之间 D. 在C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() .与
.与![]() 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,![]() ,
,![]() ,点A,C在直线
,点A,C在直线![]() 上.
上.
(1)求点C的坐标;
(2)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(3)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线![]() 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,m),B(2,m),C(3,m﹣n)(n>0)在同一个函数的图象上,这个函数可能是( )
A.y=xB.y=﹣![]() C.y=x2D.y=﹣x2
C.y=x2D.y=﹣x2
查看答案和解析>>
科目:初中数学 来源: 题型:
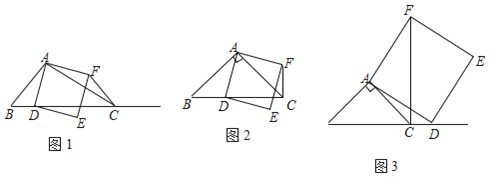
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
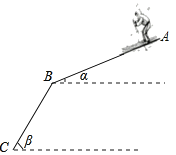
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com