
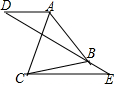
 如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.
如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$. 分析 作辅助线,构建全等三角形和直角三角形,由旋转得:∠PCE=60°,∠APC=∠E=30°,根据BE:AD=1:$\sqrt{3}$,设AD=$\sqrt{3}$x,BE=x,则AP=BE=x,根据三角函数表示PF、PH、AH、GH的长,根据PG=GH+PH列式求x的长,得BE=2,在△BGC中,利用勾股定理求得BC的长.
解答 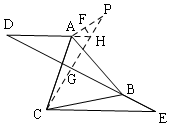 解:将△CBE绕C逆时针旋转60°到△CAP,BC与AC重合,延长DA交PC于H,过H作HF⊥AP于F,CP交DE于G,
解:将△CBE绕C逆时针旋转60°到△CAP,BC与AC重合,延长DA交PC于H,过H作HF⊥AP于F,CP交DE于G,
∴∠PCE=60°,
∵∠E=30°,
∴∠CGE=90°,
由旋转得:CE=CP,
Rt△CGE中,CE=CP=4$\sqrt{3}$,
∴CG=$\frac{1}{2}$CE=2$\sqrt{3}$,
∴GP=PC-CG=2$\sqrt{3}$,
∵AD:BE=$\sqrt{3}$:1,
设AD=$\sqrt{3}$x,BE=x,则AP=BE=x,
∵AD∥BE,
∴∠ADE=∠E=30°,
Rt△DGH中,∠DHG=60°,
由旋转得:∠APC=∠E=30°,
∴∠HAP=60°-30°=30°,
∴∠HAP=∠APC=30°,
∴AH=PH,AF=PF=$\frac{1}{2}$x,
cos30°=$\frac{PF}{PH}$,
∴PH=$\frac{\frac{1}{2}x}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$x,
∴DH=AD+AH=$\sqrt{3}$x+$\frac{\sqrt{3}}{3}$x=$\frac{4\sqrt{3}}{3}$x,
∴GH=$\frac{1}{2}$DH=$\frac{2\sqrt{3}}{3}$x,
∵PG=2$\sqrt{3}$=GH+PH,
∴2$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$x,
x=2,
∴BE=x=2,
由勾股定理得:EG=$\sqrt{E{C}^{2}-C{G}^{2}}$=$\sqrt{(4\sqrt{3})^{2}-(2\sqrt{3})^{2}}$=6,
∴BG=6-2=4,
在Rt△BGC中,BC=$\sqrt{B{G}^{2}+C{G}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$;
故答案为:$2\sqrt{7}$.
点评 本题考查了全等三角形的性质和判定、等边三角形、特殊的三角函数等知识的运用,熟练掌握特殊角的三角函数值,巧妙运用旋转作辅助线,利用等边三角形60°角将三角形平移到另一位置中,根据直角三角形中30°角所对的直角边是斜边的一半解决此题.


科目:初中数学 来源: 题型:选择题
| A. | 长方形的长是a米,宽比长短25米,则它的周长可表示为(2a-25)米 | |
| B. | 6h表示底为6,高为h的三角形的面积 | |
| C. | 10a+b表示一个两位数,它的个位数字是a,十位数字是b | |
| D. | 甲、乙两人分别从相距40千米的两地相向出发,其行走的速度分别为3千米/小时和5千米/小时,经过x小时相遇,则可列方程为3x+5x=40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
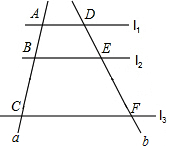 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.
如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com