
����Ŀ�������������ۺ���ֳ��������̬��ֳ����ɫ��չ��ij�����ۺ���ֳ���ƻ�����ף������ֺ̻������磬�����飬�õ�������Ϣ��
����������40 kg | ������������40 kg | |
������ | ԭ������ | ���������� |
������ | ԭ������ | ��������� |
�������10 kg�ļ������5 kg������������700Ԫ���������20 kg�ļ������15 kg������������1600Ԫ��
��1���������������ĵ��۸��Ƕ���Ԫ��
��2���־�������ף���������ƹ�90 kg�����У�����������������ڼ�����������2�����蹺�������a kg��![]() ���������ֳ����������������ܷ���W��a֮��ĺ�������ʽ��
���������ֳ����������������ܷ���W��a֮��ĺ�������ʽ��
��3���ڣ�2���������£������һ�ֹ�����ʹ�����ܷ�����ͣ����������ܷ��ã�
���𰸡���1��������۸�Ϊ50Ԫ/kg��������۸�Ϊ40Ԫ/kg����2���ٵ�![]() ʱ��
ʱ�� ![]() ���ڵ�
���ڵ�![]() ʱ��
ʱ�� ![]() ����3�������������40 kg��������50 kgʱ�������ܷ�����ͣ�����ܷ���Ϊ3000Ԫ
����3�������������40 kg��������50 kgʱ�������ܷ�����ͣ�����ܷ���Ϊ3000Ԫ
��������
��1�����������ж�Ԫһ�η�������н��
��2������������������֮��Ĺ�ϵ���г�����ʽ���飩����������������a��ȡֵ��Χ��������a��ȡֵ��Χ�ֶο����ܷ���W��a�Ĺ�ϵʽ��
��3������һ�κ��������ʣ��ֶ����ۣ�ȷ����aȡ��ֵʱ������W��ͣ�����ۺ�ȷ������W���ʱ�Ĺ�����
�⣺��1���������۸�ΪxԪ/kg��������۸�ΪyԪ/kg��
�������![]() ��
��
���![]() ��
��
�𣺼�����۸�Ϊ50Ԫ/kg��������۸�Ϊ40Ԫ/kg��
��2����������ã�![]() �����
�����![]() ��
��
��![]() ��
��
��![]() ��
��
�ٵ�![]() ʱ��
ʱ��
W����a�Ľ���ʽΪ��![]() ��
��
�ڵ�![]() ʱ��W����a�Ľ���ʽΪ��
ʱ��W����a�Ľ���ʽΪ��
![]() ��
��
��3���ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��W��a�����������
�൱![]() ʱ��W��ֵ��С����ʱ
ʱ��W��ֵ��С����ʱ![]() ��Ԫ����
��Ԫ����
�ڵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��W��a�����������
�൱![]() ʱ��W��ֵ��С����ʱ
ʱ��W��ֵ��С����ʱ![]() ��Ԫ����
��Ԫ����
��![]() ��
��
�൱���������40 kg��������50 kgʱ�������ܷ�����ͣ�����ܷ���Ϊ3000Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
![]() ����ͼʾ��д�±���
����ͼʾ��д�±���
ƽ���� | ��λ�� | ���� | |
AУ | ______ | 85 | ______ |
BУ | 85 | ______ | 100 |
![]() �����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
�����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
![]() ������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���
������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ��x���ڵ�A��B����A�ڵ�B����ࣩ��
��ͼ��x���ڵ�A��B����A�ڵ�B����ࣩ��
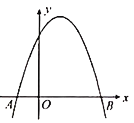
��1�����A��B�����꣬�����ݸú���ͼ��д��y��0ʱx��ȡֵ��Χ��
��2���ѵ�B����ƽ��m����λ�õ�B1������B1����ƽ��n����λ������ö��κ���ͼ���ϵĵ�B2�غϣ�����B1����ƽ��(n��6)����λ������ö��κ���ͼ���ϵĵ�B3�غϣ���֪m��0��n��0����m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��2mʱ��ˮ���4m��ˮ���½�2m��ˮ���������______m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ�����н��ۣ���
��ͼ����ͼ��ʾ�����н��ۣ���![]() ����
����![]() ����������
����������![]() ��
��![]() ����
����![]() ����
����![]() ��������ȷ����
��������ȷ����
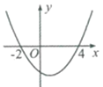
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC��8![]() cm����D���߶�BC�ϵ�һ�㣬�ֱ���BD��CDΪ����BC��ͬ�����ȱ�������ABD�͵ȱ�������CDE��AC��BE�ཻ�ڵ�P�����D�ӵ�B�˶�����Cʱ����P���˶�·�����������B��C�غϣ�Ϊ_____��
cm����D���߶�BC�ϵ�һ�㣬�ֱ���BD��CDΪ����BC��ͬ�����ȱ�������ABD�͵ȱ�������CDE��AC��BE�ཻ�ڵ�P�����D�ӵ�B�˶�����Cʱ����P���˶�·�����������B��C�غϣ�Ϊ_____��
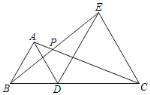
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ó��˾��������50�����г���������������Ϊÿ��ÿ��200Ԫʱ��ȫ������������ÿ���10Ԫ�����ȥ�ij��ͼ���2����
��1���������߶���Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2����˾�쵼ϣ��������ﵽ10160Ԫ������Ϊ�ܷ�ʵ�֣����ܣ������ʱ����������ܣ���˵�����ɣ�
��3�������ճ�ά��Ҫ�����ã���֪�����ÿ��ά����Ϊ100Ԫδ����ij���ά����Ϊ50Ԫ�������Ϊ����Ԫʱ����˾������ǡ��Ϊ5500Ԫ�����������橁ά���ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�κ���y=kx��6��k��0����ͼ����y�ύ�ڵ�A���뷴��������y=![]() ��x��0����ͼ���ڵ�B��4��b����
��x��0����ͼ���ڵ�B��4��b����
��1��b=�� ����k=�� ����
��2����C���߶�AB��һ�㣬����C��ƽ����y���ֱ��l���÷�����������ͼ���ڵ�D������OC��OD��BD�����ı���OCBD�����S�ı���OCBD=![]() �����C�����ꣻ
�����C�����ꣻ
��3�����ڣ�2��С���е���OCD������AB����ƽ��һ���ľ���õ���O'C'D'������O�Ķ�Ӧ��O'ǡ�����ڸ÷���������ͼ���ϣ���ͼ2�������ʱ��D�Ķ�Ӧ��D'�����꣮
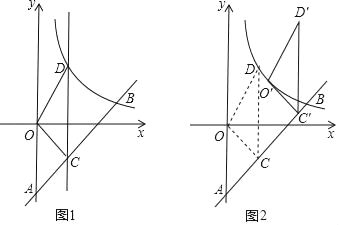
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���ͼ��Ķ�������Ϊ![]() ���������ύ��
���������ύ��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() �������Ϊ
�������Ϊ![]() .
.
��1������κ����Ľ���ʽ��
��2���ڶ��κ���ͼ��λ��![]() ���Ϸ���������������
���Ϸ���������������![]() ��
��![]() ���ҵ�
���ҵ�![]() �ڵ�
�ڵ�![]() ����࣬��
����࣬��![]() ��
��![]() ��
��![]() ��Ĵ��߽�
��Ĵ��߽�![]() ���ڵ�
���ڵ�![]() ��
��![]() ���㣬���ı���
���㣬���ı���![]() Ϊ����ʱ����þ����ܳ������ֵ��
Ϊ����ʱ����þ����ܳ������ֵ��
��3���ڣ�2���еľ����ܳ����ʱ������![]() ����֪��
����֪��![]() ��
��![]() ����һ���㣬����
����һ���㣬����![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹֱ��
��ʹֱ��![]() ��
��![]() �ֳ����Ϊ
�ֳ����Ϊ![]() �������֣������ڣ�����õ�����ꣻ�������ڣ���˵������.
�������֣������ڣ�����õ�����ꣻ�������ڣ���˵������.
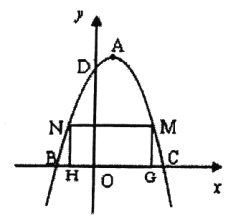 ����ͼ
����ͼ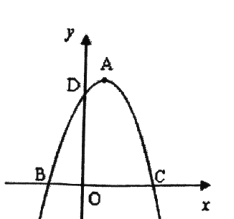
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com