
【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足![]() . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
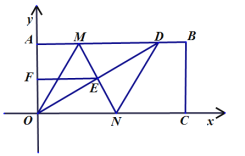
【答案】(1)6;(2)详见解析;(3)C菱形MOND=25,S菱形MOND=![]()
【解析】
(1)根据二次根式的非负性进行求解即可;
(2)根据矩形AOCB的性质以及![]() 判定四边形MOND是平行四边形,再由菱形的判定求证即可;
判定四边形MOND是平行四边形,再由菱形的判定求证即可;
(3)根据![]() 的中位线及矩形AOCB的性质构造直角三角形,设AD=x,
的中位线及矩形AOCB的性质构造直角三角形,设AD=x,![]()
利用勾股定理求出x的值,再根据菱形MOND的性质,设![]() ,
,![]() ,利用勾股定理求出y,最后根据菱形的周长及面积求法进行求解即可.
,利用勾股定理求出y,最后根据菱形的周长及面积求法进行求解即可.
(1)∵![]()
∴![]() ,
,![]()
∴![]()
∴![]() ;
;
(2)证明:∵MN垂直平分OD
∴OM=DM,DE=OE,![]()
∵四边形AOCB是矩形
∴AB∥OC
∴![]()
在![]() 和
和![]() 中
中
∴![]()
∴ME=NE
又∵DE=OE
∴四边形MOND是平行四边形
又∵OM=DM
∴四边形MOND是菱形;
(3)由(1)得OA=6
由(2)得DE=OE
又∵F为OA的中点
∴EF是![]() 的中位线,
的中位线,
∴![]()
又∵EF+OE=9,DE=OE
∴![]()
∴AD+OD =18
∵四边形AOCB是矩形
∴![]()
在![]() 中
中
设AD=x,则![]()
根据勾股定理,![]() ,解得x=8
,解得x=8
∴AD=8,OD =10
由(2)得,四边形MOND是菱形
∴OM=MD=DN=ON
设![]() ,则
,则![]()
在![]() 中,根据勾股定理
中,根据勾股定理
![]() ,解得
,解得![]()
∴![]()
∴![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 ![]()
B.﹣2 ![]()
C.﹣2 ![]() 2
2 ![]()
D.﹣2 ![]() <b<2
<b<2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.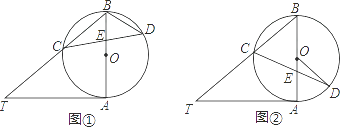
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα= ![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ![]() ,求sin2β的值.
,求sin2β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,三个半圆依次相外切,它们的圆心都在x轴的正半轴上并与直线y=![]() x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售![]() ,
,![]() 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台![]() 型空气净化器的进价与3台
型空气净化器的进价与3台![]() 型空气净化器的进价相同.
型空气净化器的进价相同.
(1)求![]() ,
,![]() 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.
(2)若商场购进这两种型号的家用空气净化器共50台,其中![]() 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过![]() 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进![]() 型家用空气净化器
型家用空气净化器![]() 台.
台.
①求![]() 的取值范围;
的取值范围;
②已知![]() 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台![]() 元;
元;![]() 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台![]() 元.若
元.若![]() ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润![]() (元)与
(元)与![]() (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com