
 在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.
在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.分析 (1)化成顶点式即可求得;
(2)根据轴对称的特点求得即可;
(3)求得顶点坐标,根据题意求得C的坐标,分两种情况表示出顶点D到点C的距离,列出不等式,解不等式即可求得.
解答 解:(1)∵抛物线y=mx2-4mx+2m-1=m(x-2)2-2m-1,
∴对称轴为x=2;
(2)∵抛物线是轴对称图形,
∴点A点B关于x=2轴对称,
∵A(-1,-2),
∴B(5,-2).
(3)∵抛物线y=mx2-4mx+2m-1=m(x-2)2-2m-1,
∴顶点D(2,-2m-1).
∵直线AB与y轴交点的纵坐标为-1,
∴C(2,-1).
∵顶点D到点C的距离大于2,
∴-2m-1+1>2或-1+2m+1>2,
∴m<-1或m>1.
点评 本题考查了二次函数的性质以及二次函数图象上点点坐标特征,把解析式化成顶点式式解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
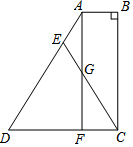 如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.
如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
在一些汉字的美术字中,有的是轴对称图形。下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有( )个
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com