
分析 先根据logNM=$\frac{lo{g}_{n}M}{lo{g}_{n}N}$(a>0,a≠1,N>0,N≠1,M>0)将所求式子化成以10为底的对数形式,再利用公式$lo{g}_{n}{n}^{a}=a$进行计算.
解答 解:先由公式logNM=$\frac{lo{g}_{n}M}{lo{g}_{n}N}$得:log1001000=$\frac{lo{g}_{10}1000}{lo{g}_{10}100}$,
由公式logaan=n得:①log101000=$lo{g}_{10}1{0}^{3}$=3;
②log10100=$lo{g}_{10}1{0}^{2}$=2;
∴log1001000=$\frac{lo{g}_{10}1000}{lo{g}_{10}100}$=$\frac{lo{g}_{10}1{0}^{3}}{lo{g}_{10}1{0}^{2}}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了实数的运算,这是一个新的定义,利用已知所给的新的公式进行计算.认真阅读,理解公式的真正意义;解决此类题的思路为:观察所求式子与公式的联系,发现1000与100都与10有关,且都能写成10的次方的形式,从而使问题得以解决.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:填空题
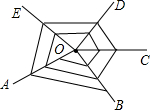 如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.
如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:选择题
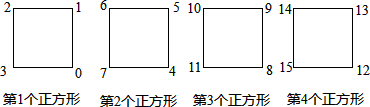
| A. | 第504个正方形的左下角 | B. | 第504个正方形的右下角 | ||
| C. | 第505个正方形的左上角 | D. | 第505个正方形的右下角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com