
 某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:
某中学为响应2017年万州区委、区府喜迎世界读书日“全面阅读,书香万州”建设的号召,在全校形成良好的人文阅读,该中学随机调查了八年级部分学生平均每天的阅读时间,统计结果如图所示:分析 (1)根据加权平均数的计算方法可以解答本题;
(2)根据统计图中的数据可以计算出该校八年级学生阅读时间不低于1.5小时的学生人数.
解答 解:(1)由题意可得,
在本次调查中,被调查学生阅读时间的平均数是:$\frac{0.5×8+1×19+1.5×10+2×3}{8+19+10+3}$=1.1,
故答案为:1.1;
(2)由题意可得,
不低于1.5小时的学生有:800×$\frac{10+3}{8+19+10+3}=260$(人),
答:不低于1.5小时的学生有260人.
点评 本题考查条形统计图、加权平均数、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
| A. | 1,-$\frac{1}{2}$ | B. | 1,-1 | C. | -1 | D. | $\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
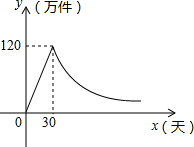 如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.
如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
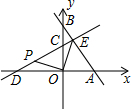 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com