
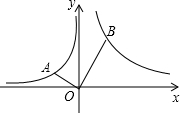
 如图A,B两点分别在反比例函数y=-$\frac{1}{x}$(x<0)和y=$\frac{k}{x}$(k>0,x>0)的图象上,连接OA、OB,若OA⊥OB,OB=2OA,则k的值为( )
如图A,B两点分别在反比例函数y=-$\frac{1}{x}$(x<0)和y=$\frac{k}{x}$(k>0,x>0)的图象上,连接OA、OB,若OA⊥OB,OB=2OA,则k的值为( )| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
分析 过A、B分别作x轴的垂线,垂足分别为E、F,先证得△AEO∽△OFB,根据相似三角形的性质得出OF=2AE,BF=2OE,设A(a,b),代入y=-$\frac{1}{x}$得出ab=-1,因为OE=-a,AE=b,所以AE•OE=-ab=1,设B(x,y),则OF=x,BF=y,即可求得k=xy=4.
解答 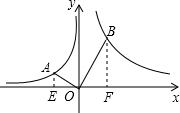 解:如图,过A、B分别作x轴的垂线,垂足分别为E、F.
解:如图,过A、B分别作x轴的垂线,垂足分别为E、F.
∵OA⊥OB,
∴∠AOE+∠BOF=90°,
∵∠AOE+∠OAE=90°,
∴∠OAE=∠BOF,
∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴$\frac{AE}{OF}$=$\frac{OE}{BF}$=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴OF=2AE,BF=2OE,
∴OF•BF=2AE•2OE=4AE•OE,
∵A点在反比例函数y=-$\frac{1}{x}$上,
设A(a,b),
∴k=ab=-1,
∵OE=-a,AE=b,
∴AE•OE=-ab=1,
设B(x,y),
∴OF=x,BF=y,
∴OF•BF=4,
∴k=xy=4.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数y=$\frac{k}{x}$(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 地区 | 北京 | 广东 | 上海 | 浙江 | 福建 | 云南 | 湖北 |
| 同比涨幅(%) | 3.3 | 3.3 | 3 | 2.8 | 2.8 | 2.8 | 2.3 |
| A. | 2.8,2.8 | B. | 2.8,2.9 | C. | 3.3,2.8 | D. | 2.8,3.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com