
【题目】如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.
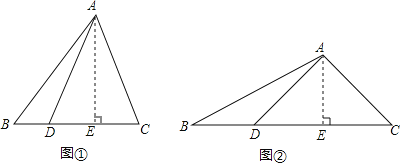
(1)填空:△ADC是 三角形;
(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;
(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.
【答案】(1)等腰(2)12(3)见解析
【解析】
试题分析:(1)根据折叠得到AD=AC,所以△ADC是等腰三角形;
(2)设CE=x,利用勾股定理得到方程132﹣x2=152﹣(14﹣x)2解得:x=5,在Rt△AEC中,由勾股定理即可解答;
(3)猜想BC、BD、AE之间的数量关系为:BC﹣BD=2AE.由△ADC是等腰三角形,又∠DAC=90°,得到△ADC是等腰直角三角形又AE是CD边上的高,所以△AED与△AEC都是等腰直角三角形,即可得到CD=2AE.由BC﹣BD=CD,即可解答.
解:(1)∵三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.
∴AD=AC,
∴△ADC是等腰三角形;
故答案为:等腰.
(2)设CE=x,则BE=14﹣x,
在Rt△AEC中,由勾股定理得:AE2=AC2﹣CE2,
∴AE2=132﹣x2
在Rt△ABE中,由勾股定理得:AE2=AB2﹣BE2,
∴AE2=152﹣(14﹣x)2
∴132﹣x2=152﹣(14﹣x)2
解得:x=5,
在Rt△AEC中,由勾股定理得:![]() .
.
(3)猜想BC、BD、AE之间的数量关系为:BC﹣BD=2AE.
证明如下:
由(1)得:△ADC是等腰三角形,又∠DAC=90°,
∴△ADC是等腰直角三角形
又AE是CD边上的高,
∴DE=CE,![]() ,
,
∴△AED与△AEC都是等腰直角三角形,
∴DE=AE=EC,即CD=2AE.
∵BC﹣BD=CD
∴BC﹣BD=2AE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
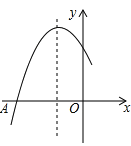
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1<y2.其中正确结论是( )
,y2)为函数图象上的两点,则y1<y2.其中正确结论是( )
A.②④ B.①④ C.①③ D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于ABCD的叙述,正确的是( )
A.若AB⊥BC,则ABCD是菱形 B.若AC⊥BD,则ABCD是正方形
C.若AC=BD,则ABCD是矩形 D.若AB=AD,则ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+8x﹣7=0,则配方正确的是( )
A.(x+4)2=23
B.(x﹣4)2=23
C.(x﹣8)2=49
D.(x+8)2=64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com