
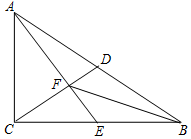
 如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE•CB.
如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE•CB.分析 (1)先根据题意得出△ACB∽△ECA,再由直角三角形的性质得出CD=AD,由∠CAD+∠ABC=90°可得出∠ACD+∠EAC=90°,进而可得出∠AFC=90°;
(2)根据AE⊥CD可得出∠EFC=90°,∠ACE=∠EFC,故可得出△ECF∽△EAC,再由点E是BC的中点可知CE=BE,故$\frac{BE}{EA}=\frac{EF}{BE}$,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
解答 证明:(1)∵AC2=CE•CB,
∴$\frac{AC}{CE}=\frac{CB}{AC}$.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
(2)∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴$\frac{EC}{EA}=\frac{EF}{EC}$
∵点E是BC的中点,
∴CE=BE,
∴$\frac{BE}{EA}=\frac{EF}{BE}$
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的判定定理是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 如图,P是反比例函数y=$\frac{k}{x}$图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积我3,求该反比例函数的表达式是△OPQ的面积.
如图,P是反比例函数y=$\frac{k}{x}$图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积我3,求该反比例函数的表达式是△OPQ的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
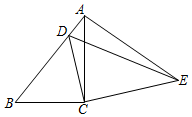 如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 投掷一枚均匀的硬币,正面朝上的概率是$\frac{1}{2}$ | |
| B. | 投掷一枚图钉,钉尖朝上、朝下的概率一样 | |
| C. | 投掷一枚均匀的骰子,每一种点数出现的概率都是$\frac{1}{6}$,所以每投6次,一定会出现一次“l点” | |
| D. | 投掷一枚均匀的骰子前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com