
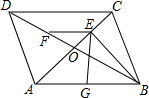
 如图所示,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点.证明:
如图所示,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点.证明:分析 (1)由平行四边形的性质和已知条件证得BC=BO,根据等腰三角形的性质得出结论;
(2)直角三角形斜边上的中线等于斜边的一半求出EG=$\frac{1}{2}$AB,由三角形中位线定理求得EF=$\frac{1}{2}$DC,根据AB=DC即可得到结论.
解答  证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,BD=2OB=2OD,
∵BD=2AD,
∴OB=BC,
∵E为OB中点,
∴BE⊥AC(三线合一定理);
(2)∵∠AEB=90°,
∵G为AB中点,
∴AB=2EG(直角三角形斜边上的中线等于斜边的一半),
∵AB=CD,
∴CD=2EG,
∵E、F分别是OC、OD中点,
∴CD=2EF,
∴EG=EF.
点评 本题考查了平行四边形性质,直角三角形斜边上中线性质,等腰三角形性质,三角形的中位线性质的应用,关键是求出EG=$\frac{1}{2}$AB,题目比较好,综合性比较强.


科目:初中数学 来源: 题型:解答题
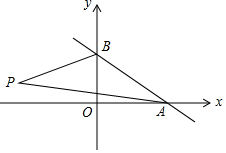 如图,已知直线l1经过点A(2,0)与点B(0,1),如果在第二象限内有一点P(a,$\frac{1}{2}$),且△APB的面积为3,求a的值.
如图,已知直线l1经过点A(2,0)与点B(0,1),如果在第二象限内有一点P(a,$\frac{1}{2}$),且△APB的面积为3,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 写出下列命题的已知、求证,并完成证明过程.
写出下列命题的已知、求证,并完成证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
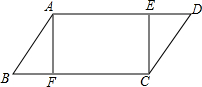 如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:
如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
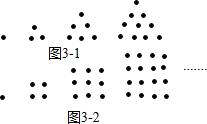 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:
古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com