
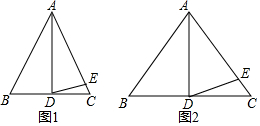
分析 (1)等腰三角形三线合一,所以∠DAE=30°,又因为AD=AE,所以∠ADE=∠AED=75°,所以∠DEC=15°;
(2)同理,易证∠ADE=70°,所以∠DEC=20°;
(3)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,
进而得出∠BAD=2∠CDE.
解答 解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°;
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°;
(3)∠BAD=2∠EDC(或∠EDC=$\frac{1}{2}$∠BAD);理由如下:
∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE.
故答案为:15°;20°.
点评 本题考查了等腰三角形三线合一的性质,等边对等角的性质,三角形的外角性质进行推理的能力,熟记性质是解题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:选择题
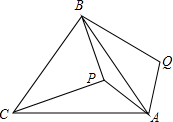 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到AQ,连接BQ.若PA=6,PB=8,PC=10,则三角形PBQ的面积为( )
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到AQ,连接BQ.若PA=6,PB=8,PC=10,则三角形PBQ的面积为( )| A. | 12 | B. | 40 | C. | 30 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
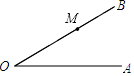 如图,∠AOB=30°,点M在OB上,且OM=5cm,以M为圆心,r为半径画圆,试讨论r的大小与所画⊙M和射线OA的公共点个数之间的对应关系.
如图,∠AOB=30°,点M在OB上,且OM=5cm,以M为圆心,r为半径画圆,试讨论r的大小与所画⊙M和射线OA的公共点个数之间的对应关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当m=-2时,函数图象与x轴没有交点 | |
| B. | 当m=1时,函数图象过点(-1,1) | |
| C. | 若m<0,则当x≤1时,y随x的增大而增大 | |
| D. | 若m>0,则当x≥1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 905×1010 | B. | 90.5×1011 | C. | 9.05×1012 | D. | 0.95×1013 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
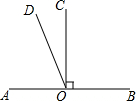 如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )
如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com