
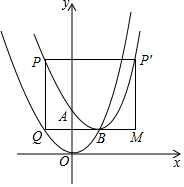
 如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).
如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).分析 (1)利用待定系数法即可解决问题.
(2)①由题意抛物线的解析式为y=$\frac{1}{2}$x2,设P(m,$\frac{1}{2}$m2-2m+4),则Q(m,$\frac{1}{2}$m2),由点B(2,2)在边QM上,可得$\frac{1}{2}$m2=2,解方程即可.
②分两种情形讨论,如图1中,当-2$\sqrt{2}$≤m≤-2时,重叠部分是△AEF.如图2中,当-2<m≤0时,重叠部分是四边形AEFB,
(3)当点P与A重合时,易知AP′=4,OA=4,此时四边形PP′MQ是面积为16的正方形,点Q与O重合,Q(0,0),把Q(0,0)代入y=$\frac{1}{2}$(x-h)2+h,即可解决问题.
解答 解:(1)∵抛物线y=a(x-2)2+2经过点A(0,4),0
∴4=4a+2,
∴a=$\frac{1}{2}$.
(2)①由题意抛物线的解析式为y=$\frac{1}{2}$x2,设P(m,$\frac{1}{2}$m2-2m+4),则Q(m,$\frac{1}{2}$m2),
∵点B(2,2)在边QM上,
∴$\frac{1}{2}$m2=2,
∴m=-2或2(舍弃),
②如图1中,当-2$\sqrt{2}$≤m≤-2时,重叠部分是△AEF.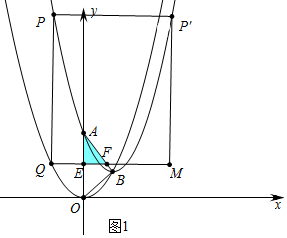
l=2(4-$\frac{1}{2}$m2)+$\sqrt{2}$(4-$\frac{1}{2}$m2)=-(1+$\frac{\sqrt{2}}{2}$)m2+8+4$\sqrt{2}$,
如图2中,当-2<m≤0时,重叠部分是四边形AEFB,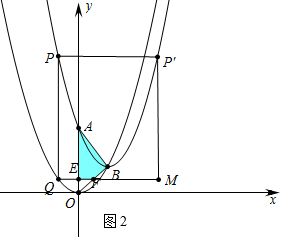
l=△ABC的周长-△OEF的周长=4+4$\sqrt{2}$-(2×$\frac{1}{2}$m2+$\sqrt{2}$×$\frac{1}{2}$m2)=-(1+$\frac{\sqrt{2}}{2}$)m2+4+4$\sqrt{2}$,
综上所述,l=$\left\{\begin{array}{l}{-(1+\frac{\sqrt{2}}{2}){m}^{2}+8+4\sqrt{2}}&{(-2\sqrt{2}≤m≤-2)}\\{-(1+\frac{\sqrt{2}}{2}){m}^{2}+4+4\sqrt{2}}&{(-2<m≤0)}\end{array}\right.$.
(3)如图3中,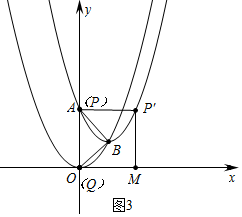
当点P与A重合时,易知AP′=4,∵A(0,4),
∴OA=4,此时四边形PP′MQ是面积为16的正方形,
∴点Q与O重合,Q(0,0),
把Q(0,0)代入y=$\frac{1}{2}$(x-h)2+h,得到h=0.
点评 本题考查二次函数综合题、矩形的性质、正方形的判定和性质、等腰直角三角形的性质和判定、多边形的周长等知识,解题的关键是灵活应用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 请把下列解题过程补充完整并在括号中注明理由.如图,EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD.
请把下列解题过程补充完整并在括号中注明理由.如图,EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
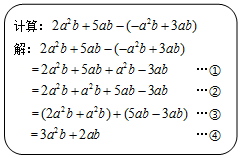
| A. | ①:去括号法则 | B. | ②:加法交换律 | ||
| C. | ③:等式的基本性质 | D. | ④:合并同类项法则 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
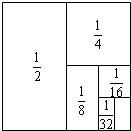 如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.
如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com