【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒，…，
（1）按此规律，图案⑦需____根火柴棒；第n个图案需____根火柴棒．
（2）用2018根火柴棒能按规律拼搭而成一个图案？若能，说明是第几个图案：若不可能，请说明理由．
【答案】（1）图案⑦需50根火柴棒；图案n需火柴棒7n+1根；（2）2017是第288个图案．理由见解析.
【解析】
（1）根据图案①、②、③中火柴棒的数量可知，第1个图形中火柴棒有8根，每多一个多边形就多7根火柴棒，由此可知第n个图案需火柴棒8+7（n-1）=7n+1根，令n=7可得答案．
（2）令8+7（n-1）=7n+1=2017求得n值即可．
解:（1）∵图案①需火柴棒：8根；
图案②需火柴棒：8+7=15根；
图案③需火柴棒：8+7+7=22根；
…
∴图案n需火柴棒：8+7（n-1）=7n+1根；
当n=7时，7n+1=7×7+1=50，
∴图案⑦需50根火柴棒；
（2）令7n+1=2017，
解得n=288，
故2017是第288个图案．
科目：初中数学 来源： 题型：
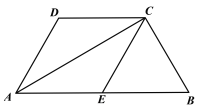
【题目】已知，四边形ABCD中，AB∥CD，AB=2CD，E为AB的中点，AC为对角线，AC⊥BC.
（1）求证：四边形AECD是菱形.
（2）若∠DAE=60°，AE=2，求菱形AECD的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A（0，4），B（2，0），点C在第一象限，若以A、B、C为顶点的三角形与△AOB相似（不包括全等），则点C的个数是（ ）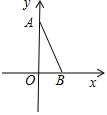 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各式中：
①由3x＝﹣4系数化为1得x＝﹣
；
②由5＝2﹣x移项得x＝5﹣2；
③由
去分母得2（2x﹣1）＝1+3（x﹣3）；
④由2（2x﹣1）﹣3（x﹣3）＝1去括号得4x﹣2﹣3x﹣9＝1．
其中正确的个数有（ ）
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）“六·一”儿童节前，某玩具商店根据市场调查，用2500元购进一批儿童玩
具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5
倍，但每套进价多了10元．
（1）求第一批玩具每套的进价是多少元？
（2）如果这两批玩具每套售价相同，且全部售完后总利润不低于25%，那么每套售价至少是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
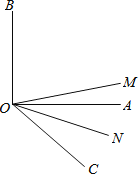
【题目】已知：如图，ON平分∠AOC，OM平分∠BOC，∠AOB=90°
（1）若∠AOC=40°，求∠AOM和∠MON的大小；
（2）当锐角∠AOC的度数发生改变时，∠MON的大小是否发生改变？如不会改变，请写出∠MON的大小，并写出推理过程；如会改变，也请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为满足同学们课外阅读的需求，某中学图书馆向出版社邮购科普系列图书，每本书单价为16元，书的价钱和邮费是通过邮局汇款，相关的书价折扣、邮费和汇款的汇费如下表所示（总费用=总书价+总邮费+总汇费）
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 （汇款不足100元时按100元汇款收汇费） |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 （汇款不足100元的部分不收汇费） |
（1）若一次邮购7本，共需总费用为 元．
（2）已知学校图书馆需购图书的总数是10的整倍数，且超过10本．
①若分次邮购，分别汇款，每次邮购10本，总费用为1064元时，共邮购了多本图书？
②若你是学校图书馆负责人，从节约的角度出发，在“每次邮购10本“与“一次性邮购”这两种方式中选择一种，你会选择哪一种？计算并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率= | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
（1）请估计：当n很大时，摸到白球的频率将会接近多少？(精确到0.1)
（2）假如你摸一次，你摸到白球的概率P(白球)是多少？
（3）试估算盒子里黑、白两种颜色的球各有多少只？
查看答案和解析>>
科目：初中数学 来源： 题型：
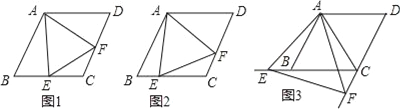
【题目】已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．
（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系为： ；
（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；
（3）求△AEF周长的最小值。
(4) 如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
