
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
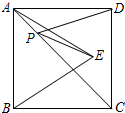 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.
已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )| A. | 9:4 | B. | 3:2 | C. | $\sqrt{3}:\sqrt{2}$ | D. | $3\sqrt{3}:2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为$\widehat{BC}$的中点.
如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为$\widehat{BC}$的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题:
从化市某中学初三(1)班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况,特对本班50名同学们进行调查,根据全班同学提出的3个主要观点:A高中,B中技,C就业,进行了调查(要求每位同学只选自己最认可的一项观点);并制成了扇形统计图(如图).请回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com