
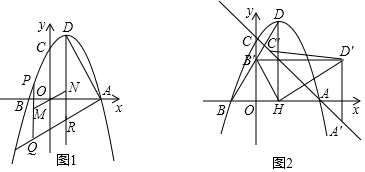
分析 (1)求出直线AD的解析式,根据AR⊥AD,再求出直线AR的解析式即可解决问题.
(2)如图1中,设P(m,-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+3$\sqrt{3}$),则Q(m,$\frac{\sqrt{3}}{3}$m-2$\sqrt{3}$),M(m,-$\frac{\sqrt{3}}{8}$m2+$\frac{2\sqrt{3}}{3}$m+$\frac{\sqrt{3}}{2}$),构建二次函数,利用二次函数的性质求出点P坐标,如图2中,点P关于对称轴的对称点为M,点M关于y轴的对称点为N,连接AN交y轴于F,连接FM交对称轴于E,此时PE+EF+AF最小.分别求出直线AN、FM的解析式即可解决问题.
(3)分三种情形讨论即可①当C′D′=A′C′=3$\sqrt{7}$时.②当A′D′=A′C′=3$\sqrt{7}$时.③当D′C′=D′A′时分别求解即可.
解答 解:(1)对于抛物线y=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$,令y=0,得-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$=0,解得x=-2或6,
∴B(-2,0),A(6,0),
∵y=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(x-2)2+4$\sqrt{3}$,
∴抛物线顶点D坐标为(2,4$\sqrt{3}$),对称轴x=2,
设直线AD的解析式为y=kx+b则有$\left\{\begin{array}{l}{2k+b=4\sqrt{3}}\\{6k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=6\sqrt{3}}\end{array}\right.$,
∴直线AD的解析式为y=-$\sqrt{3}$x+6$\sqrt{3}$,
∵AR⊥AD,
∴直线AR的解析式为y=$\frac{\sqrt{3}}{3}$x-2$\sqrt{3}$,
∴点R坐标(2,-$\frac{4\sqrt{3}}{3}$).
(2)如图1中,设P(m,-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m+3$\sqrt{3}$),则Q(m,$\frac{\sqrt{3}}{3}$m-2$\sqrt{3}$),M(m,-$\frac{\sqrt{3}}{8}$m2+$\frac{2\sqrt{3}}{3}$m+$\frac{\sqrt{3}}{2}$),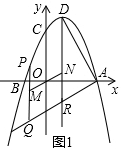
由(1)可知tan∠DAB=$\frac{4\sqrt{3}}{4}$=$\sqrt{3}$,
∴∠DAB=60°,∵∠DAQ=90°,
∴∠BAQ=30°,
∴平行四边形MNRQ周长=2(-$\frac{\sqrt{3}}{8}$m2+$\frac{2\sqrt{3}}{3}$m+$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{3}$m+2$\sqrt{3}$)+2(2-m)•cos30°=-$\frac{\sqrt{3}}{4}$m2-$\frac{\sqrt{3}}{3}$m+7$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(m+$\frac{2}{3}$)2+$\frac{64\sqrt{3}}{9}$,
∴m=-$\frac{2}{3}$时,平行四边形MNRQ周长最大,
此时P(-$\frac{2}{3}$,$\frac{20\sqrt{3}}{9}$),
如图2中,点P关于对称轴的对称点为M,点M关于y轴的对称点为N,连接AN交y轴于F,连接FM交对称轴于E,此时PE+EF+AF最小.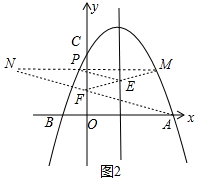
理由:PE+EF+AF=EM+FE+AF=FM+AF=FN+AF=AN,
根据两点之间线段最短,可知此时PE+EF+AF最小.
∵M($\frac{14}{3}$,$\frac{20\sqrt{3}}{9}$),N(-$\frac{14}{3}$,$\frac{20\sqrt{3}}{9}$),
∴直线AN的解析式为y=-$\frac{5\sqrt{3}}{24}$x+$\frac{5\sqrt{3}}{4}$,
∴点F坐标(0,$\frac{5\sqrt{3}}{4}$),
∴直线FM的解析式为y=$\frac{5\sqrt{3}}{24}$x+$\frac{5\sqrt{3}}{4}$,
∴点E坐标(2,$\frac{5\sqrt{3}}{3}$).
(3)能.如图3中,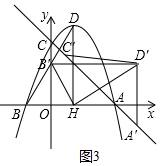
由题意可知,∠DBH=60°,∵HB=HB′,
∴△BHB′是等边三角形,
∴BB′=BH=HB′=DB′=4,∠D′B′H=∠BHB′=60°,
∴B′D′∥x轴,D′(8,2$\sqrt{3}$),AC=$\sqrt{O{C}^{2}+O{A}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{6}^{2}}$=3$\sqrt{7}$,
∵C(0,3$\sqrt{3}$),A(6,0),
∴直线AC的解析式为y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$,
①当C′D′=A′C′=3$\sqrt{7}$时,设C′(m,-$\frac{\sqrt{3}}{2}$m+3$\sqrt{3}$),
∴(8-m)2+(2$\sqrt{3}$+$\frac{\sqrt{3}}{2}$m-3$\sqrt{3}$)2=(3$\sqrt{7}$)2,
解得m=$\frac{38-2\sqrt{333}}{7}$或$\frac{38+2\sqrt{333}}{7}$,
∴C′($\frac{38-2\sqrt{333}}{7}$,$\frac{2\sqrt{3}+3\sqrt{111}}{7}$)或($\frac{38+2\sqrt{333}}{7}$,$\frac{2\sqrt{3}-3\sqrt{111}}{7}$),
把点C′向下平移3$\sqrt{3}$个单位,向右平移6个单位得到A′,
∴此时A′的坐标为($\frac{80-2\sqrt{333}}{7}$,$\frac{-19\sqrt{3}+3\sqrt{111}}{7}$)或($\frac{80+2\sqrt{333}}{7}$,$\frac{-19\sqrt{3}-3\sqrt{111}}{7}$).
②当A′D′=A′C′=3$\sqrt{7}$时,设A′(n,-$\frac{\sqrt{3}}{2}$n+3$\sqrt{3}$),
∴(8-n)2+(2$\sqrt{3}$+$\frac{\sqrt{3}}{2}$n-3$\sqrt{3}$)2=(3$\sqrt{7}$)2,
解得n=$\frac{38-2\sqrt{333}}{7}$或$\frac{38+2\sqrt{333}}{7}$,
∴A′($\frac{38-2\sqrt{333}}{7}$,$\frac{2\sqrt{3}+3\sqrt{111}}{7}$)或($\frac{38+2\sqrt{333}}{7}$,$\frac{2\sqrt{3}-3\sqrt{111}}{7}$),
③当D′C′=D′A′时,作D′H⊥A′C′于H,则直线D′H的解析式为y=$\frac{2\sqrt{3}}{3}$x-$\frac{10\sqrt{3}}{3}$,
由$\left\{\begin{array}{l}{y=\frac{2\sqrt{3}}{3}x-\frac{10\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{2}x+3\sqrt{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{38}{7}}\\{y=\frac{2\sqrt{3}}{7}}\end{array}\right.$,
∴点H坐标($\frac{38}{7}$,$\frac{2\sqrt{3}}{7}$),
把点H向下平移$\frac{3\sqrt{3}}{2}$,向右平移3个单位即可得到A′($\frac{59}{7}$,-$\frac{17\sqrt{3}}{14}$).
综上所述,满足条件的点A′的坐标为($\frac{80-2\sqrt{333}}{7}$,$\frac{-19\sqrt{3}+3\sqrt{111}}{7}$)或($\frac{80+2\sqrt{333}}{7}$,$\frac{-19\sqrt{3}-3\sqrt{111}}{7}$)或($\frac{38-2\sqrt{333}}{7}$,$\frac{2\sqrt{3}+3\sqrt{111}}{7}$)或($\frac{38+2\sqrt{333}}{7}$,$\frac{2\sqrt{3}-3\sqrt{111}}{7}$)或($\frac{38}{7}$,$\frac{2\sqrt{3}}{7}$).
点评 本题考查二次函数综合题、一次函数的应用、平行四边形的性质、等腰三角形的判定和性质、两点间距离公式等知识,解题的关键是灵活运用所学知识解决问题,学会利用对称解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
| 种子个数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 发芽种子个数 | 94 | 187 | 282 | 338 | 435 | 530 | 624 | 718 | 814 | 901 |
| 发芽种子频率 | 0.940 | 0.935 | 0.940 | 0.845 | 0.870 | 0.883 | 0.891 | 0.898 | 0.904 | 0.901 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
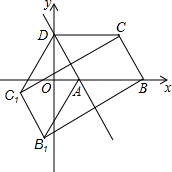 如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.
如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
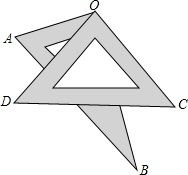 如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O
如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O查看答案和解析>>
科目:初中数学 来源: 题型:选择题
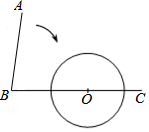 如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )| A. | 40°或80° | B. | 50°或110° | C. | 50°或100° | D. | 60°或120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外作等腰直角三角形ABE和等腰直角三角形ACF,FN平分∠AFC交AC于点N,D为BC的中点,DM∥AC交AB于点M,连接DE、DF、EF、EM.对于以下结论:①DM=FN;②S四边形ACDM=3S△BDM;③DE=DF;④∠EFD=$\frac{1}{2}$∠EDF.其中正确结论的个数是
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外作等腰直角三角形ABE和等腰直角三角形ACF,FN平分∠AFC交AC于点N,D为BC的中点,DM∥AC交AB于点M,连接DE、DF、EF、EM.对于以下结论:①DM=FN;②S四边形ACDM=3S△BDM;③DE=DF;④∠EFD=$\frac{1}{2}$∠EDF.其中正确结论的个数是| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com