
【题目】节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 今年的销售价格 | 2 |
那么新款B型节能电动车至少要购进多少辆?
【答案】(1)今年A型车每辆售价0.8万元,见解析;(2)新款B型节能电动车至少要购进12辆
【解析】
(1)设今年A型节能电动车每辆售价x万元,则去年售价每辆为(x+0.2)万元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进B型节能电动车a辆,则A型节能电动车![]() 辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
解:(1)设今年A型车每辆售价x万元,则去年售价每辆为(x+0.2)万元,由题意,得
![]() =
=![]() ,
,
解得:x=0.8.
经检验,x=0.8是原方程的根.
答:今年A型车每辆售价0.8万元;
(2)设今年新进B型节能电动车a辆,则A型节能电动车![]() 辆,获利y元,依题意得
辆,获利y元,依题意得
y=a(20000﹣0.7×10000)+![]() (8000﹣0.55×10000)+1500×
(8000﹣0.55×10000)+1500×![]() ≥180000,
≥180000,
解得 a≥12.
因为a是整数,所以a=12.
答:新款B型节能电动车至少要购进12辆.


科目:初中数学 来源: 题型:
【题目】随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,推动了快递行业的高速发展.据调查,岳阳市某家小型快递公司,今年1月份与3月份完成投递的快递总件数分别为8万件和9.68万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率.
(2)如果平均每人每月可投递快递0.4万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,![]() ,求证:四边形ABCD与四边形A1B1C1D1相似.
,求证:四边形ABCD与四边形A1B1C1D1相似.

(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFDE的面积为S2,若四边形ABFE与四边形EFCD相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
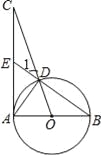
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
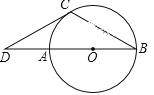
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为60元/件的夏季服装,规定试销期间销售单价不低于成本单价,且获利不得高于成本的50%,经市场试销调研发现,日销售量y(件)与售价x(元/件)符合一次函数y=kx+b,且当售价80元/件时,日销量为70件,当售价为70元件时,日销量为80件
(1)求一次函数y=kx+b的表达式;
(2)若该商场每天获得利润为w元,试写出利润w与售价x之间的关系式,并求出售价定为多少元时,商场每天可获得最大利润,最大利润是多少元?(利润=销售收入﹣进货成本,不含其他支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com