
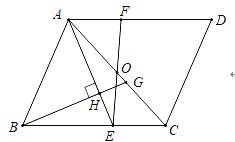
【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点F.过点
于点F.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)见解析;(2)①见解析,②![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据平行四边形的性质得到∠OAF=∠OCE,证明△OAF≌△OCE,根据全等三角形的对应边相等证明结论;
(2)①过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,根据三角形的外角性质得到∠BAG=∠BGA;
②证明△AME≌△BNG,根据全等三角形的性质得到ME=NG,根据等腰直角三角形的性质得到BE=![]() GC,根据(1)中结论证明即可.
GC,根据(1)中结论证明即可.
(1)证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
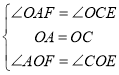 ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
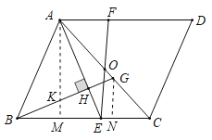
(2)①过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ;
;
②![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
在等腰![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】10袋小麦以每袋150干克为准,超过的干克数记为正数,不足的干克数记为负数,分别记为:-6,-3,-1,-2,+7,+3,+4,-3,-2,0.
(1)在这10袋小麦中,最重和最轻的分别重多少干克?
(2)与标准质量相比较,这10袋小麦超过或不足多少干克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若点E是![]() 的中点,求∠F的度数;
的中点,求∠F的度数;
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BEEF的值最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
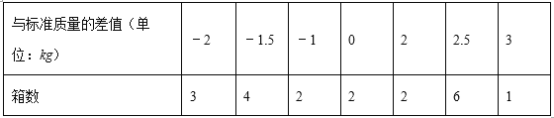
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:
①小明从家出发5分钟时乘上公交车 ②公交车的速度为400米/分钟
③小明下公交车后跑向学校的速度为100米/分钟 ④小明上课没有迟到
其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这串数是由小明按照一定规则写下来的,他第一次写下“
这串数是由小明按照一定规则写下来的,他第一次写下“![]() ,
,![]() ”,第二次接着写“
”,第二次接着写“![]() ,
,![]() ”,第三次接着写“
”,第三次接着写“![]() ,
,![]() ”,第四次接着写“
”,第四次接着写“![]() ,
,![]() ”,沿着这个规则,那么接着“
”,沿着这个规则,那么接着“![]() ,
,![]() ”后面的三个数应为( )
”后面的三个数应为( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=x的图象与函数y=![]() (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).
(1)求m,k的值;
(2)直线y=4与函数y=x的图象相交于点A,与函数y=![]() (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数.如,[π]=3,[2]=2,[﹣2.1]=﹣3.则下列结论:
①[﹣x]=﹣[x];
②若[x]=n,则x的取值范围是n≤x<n+1;
③当﹣1<x<1时,[1+x]+[1﹣x]的值为1或2;
④x=﹣2.75是方程4x﹣2[x]+5=0的唯一一个解.
其中正确的结论有_____(写出所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com