
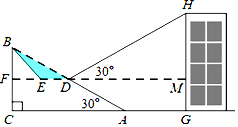
 如图,已知斜坡AB长为80米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,已知斜坡AB长为80米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.分析 (1)根据题意得出∠BEF=45°,解直角△BDF,求出BF,DF,进而得出EF的长,即可得出答案;
(2)利用在Rt△DPA中,DP=$\frac{1}{2}$AD,以及PA=AD•cos30°进而得出DM的长,利用HM=DM•tan30°得出即可.
解答 解:(1)∵修建的斜坡BE的坡角为45°,
∴∠BEF=45°,
∵∠DAC=∠BDF=30°,AD=BD=40,
∴BF=EF=$\frac{1}{2}$BD=20,DF=$20\sqrt{3}$,
∴DE=DF-EF=20$\sqrt{3}$-20,
∴平台DE的长为(20$\sqrt{3}$-20)米;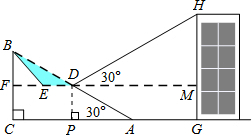 (2)过点D作DP⊥AC,垂足为P.
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=$\frac{1}{2}$AD=$\frac{1}{2}$×40=20,PA=AD•cos30°=20$\sqrt{3}$,
在矩形DPGM中,MG=DP=20,DM=PG=PA+AG=20$\sqrt{3}$+36.
在Rt△DMH中,HM=DM•tan30°=(20$\sqrt{3}$+36)×$\frac{\sqrt{3}}{3}$=20+12$\sqrt{3}$,
则GH=HM+MG=20+12$\sqrt{3}$+20=40+12$\sqrt{3}$.
答:建筑物GH高为(40+12$\sqrt{3}$)米.
点评 此题主要考查了解直角三角形的应用-坡度坡角问题以及仰角俯角问题,根据图形构建直角三角形,进而利用锐角三角函数得出是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 做100次这种实验,事件A必发生5次 | |
| B. | 做100次这种实验,事件A不可能发生5次 | |
| C. | 做1000次这种实验,事件A必发生50次 | |
| D. | 大量重复做这种实验,事件A平均每100次发生5次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.
如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com