
 “折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.
“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.  阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
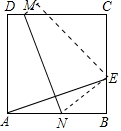 如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.
如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
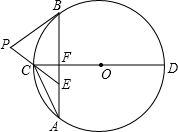 如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com