
已知:抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),C(0,﹣3).
(1)求抛物线的表达式及顶点D的坐标;
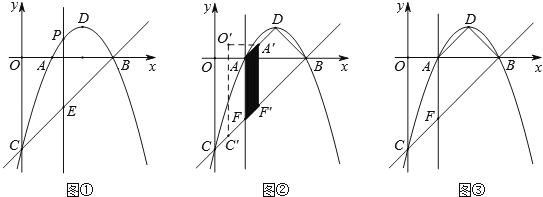
(2)如图①,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线,交直线BC于点E.是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,请说明理由;
(3)如图②,过点A作y轴的平行线,交直线BC于点F,连接DA、DB.四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点B重合时立即停止运动.设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S,请求出S与t的函数关系式.
解:(1)∵抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),C(0,﹣3).
∴ ,
,
解得 ,
,
∴抛物线的解析式:y=﹣x2+4x﹣3,
由y=﹣x2+4x﹣3=﹣(x﹣2)2+1,可知:顶点D的坐标(2,1).
(2)存在;
设直线BC的解析式为:y=kx+b,
则 ,
,
解得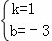 ,
,
∴直线BC的解析式为y=x﹣3,
设P(x,﹣x2+4x﹣3),则F(x,x﹣3),
∴PF=(﹣x2+4x﹣3)﹣(x﹣3)=﹣x2+3x=﹣(m﹣)2+,
∴当x=时,PF有最大值为.
∴存在一点P,使线段PE的长最大,最大值为.
(3)∵A(1,0)、B(3,0)、D(2,1)、C(0,﹣3),
∴可求得直线AD的解析式为:y=x﹣1;
直线BC的解析式为:y=x﹣3.
∴AD∥BC,且与x轴正半轴夹角均为45°.
∵AF∥y轴,∴F(1,﹣2),∴AF=2.
①当0≤t≤ 时,如答图1﹣1所示.
时,如答图1﹣1所示.
此时四边形AFF′A′为平行四边形.
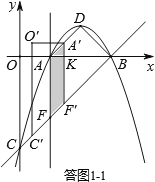
设A′F′与x轴交于点K,则AK=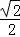 AA′=
AA′=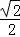 t.
t.
∴S=S▱AFF′A′=AF•AK=2×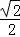 t=
t=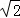 t;
t;
②当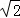 <t≤2
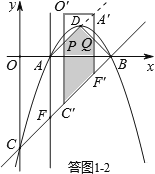
<t≤2 时,如答图1﹣2所示.
时,如答图1﹣2所示.
设O′C′与AD交于点P,A′F′与BD交于点Q,
则四边形PC′F′A′为平行四边形,△A′DQ为等腰直角三角形.
∴S=S▱PC′F′A′﹣S△A′DQ=2×1﹣(t﹣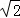 )2=﹣t2+
)2=﹣t2+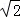 t+1;
t+1;
③当2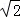 <t≤3
<t≤3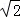 时,如答图1﹣3所示.
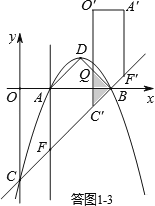
时,如答图1﹣3所示.
设O′C′与BD交于点Q,则△BC′Q为等腰直角三角形.
∵BC=3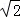 ,CC′=t,∴BC′=3
,CC′=t,∴BC′=3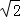 ﹣t.
﹣t.
∴S=S△BC′Q=(3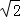 ﹣t)2=t2﹣3
﹣t)2=t2﹣3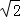 t+9.
t+9.
综上所述,S与t的函数关系式为:
S=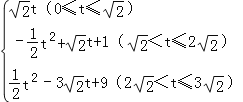


科目:初中数学 来源: 题型:
如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
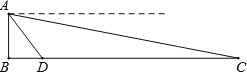
如图,王老师站在湖边度假村的景点A处,观察到一只水鸟由岸边D处飞向湖中小岛C处,点A到DC所在水平面的距离AB是15米,观测水鸟在点D和点C处时的俯角分别为53°和11°,求C、D两点之间距离.(精确到0.1.参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin11°≈0.19,cos11°≈0.98,tan11°≈0.19)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com