
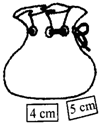
 如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:
如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:分析 (1)根据题意可以写出所有的可能性,根据三角形两边之和大于第三边可以判断有几种可能性符合要求,从而可以求得这三条线段能构成三角形的概率;
(2)根据等腰三角形的定义可以得到哪几组符号要求,从而可以得到这三条线段能构成等腰三角形的概率.
解答 解:(1)由题意可得,
随机从袋内取出一张卡片,与口袋外两张卡片放在一起的所有可能性是:
(1、4、5),(2、4、5),(3、4、5),(4、4、5),(5、4、5),
∵1+4=5,则(1、4、5)这组不能构成三角形,
∴这三条线段能构成三角形的概率是$\frac{4}{5}$;
(2)由题意可得(4、4、5),(5、4、5)这两组可以构成等腰三角形,
∴这三条线段能构成等腰三角形的概率是$\frac{2}{5}$.
点评 本题考查列表法与树状图法、三角形的三边关系、等腰三角形的判定,解题的关键是明确题意,可以写出所有的可能性,求出相应的概率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-2 | B. | 2.5×10-3 | C. | 2.5×10-2 | D. | 2.5×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | B. | $\frac{180}{x}$-$\frac{180}{x+2}$=3 | C. | $\frac{180}{x+2}$-$\frac{180}{x}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com