
【题目】已知△ABC是等边三角形,点D为平面内一点,连接DB、DC,∠BDC=120°.
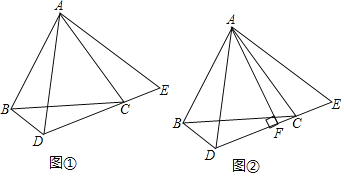
(1)如图①,当点D在BC下方时,连接AD,延长DC到点E,使CE=BD,连接AE.
①求证:△ABD≌△ACE;
②如图②,过点A作AF⊥DE于点F,直接写出线段AF、BD、DC间的数量关系;
(2)若AB=2![]() ,DC=6,直接写出点A到直线BD的距离.
,DC=6,直接写出点A到直线BD的距离.
【答案】(1)①证明见解析;②AF=![]() (CD+BD);(2)4
(CD+BD);(2)4![]() 或
或![]()
【解析】
(1)①由等边三角形的性质可得AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,由四边形的内角和定理可得∠ACE=∠ABD,由“SAS”可证△ABD≌△ACE;
②由全等三角形的性质可得AD=AE,∠BAD=∠CAE,可证△ADE是等边三角形,可得AF=![]() DF=
DF=![]() AD,即可求解;
AD,即可求解;
(2)分两种情况讨论,当点D在BC下方时,利用全等三角形的性质和勾股定理可求点A到直线BD的距离;当点D在BC上方时,过点C作CH⊥BD交BD延长线于H,过点D作DF⊥BC于F,过点A作AN⊥BD,交BD的延长线于N,利用面积法可求DF的长,由三角函数可求解.
证明:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,
∵∠ABD+∠BDC+∠ACD+∠BAC=360°,∠BDC=120°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ACE=∠ABD,
又∵AB=AC,BD=CE,
∴△ABD≌△ACE(SAS);
②∵△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∴∠DAC+∠CAE=∠DAC+∠BAD=∠BAC=60°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴AD=ED,
∵AF⊥DE,AD=AE,
∴DF=![]() DE=
DE=![]() AD,∠DAF=30°,
AD,∠DAF=30°,
∴AF=![]() DF=
DF=![]() AD,
AD,
∵DE=CD+CE=CD+BD,
∴AF=![]() AD=
AD=![]() (CD+BD);
(CD+BD);
(2)如图②,若点D在BC下方时,
∵△ABD≌△ACE,
∴点A到直线BD的距离=点A到直线CE的距离,
设DF=x,则AF=![]() x,
x,
∵AC2=AF2+CF2,
∴52=3x2+(6﹣x)2,
∴x1=4,x2=﹣1(舍去),
∴AF=4![]() ,
,
如图3,若点D在BC上方时,过点C作CH⊥BD交BD延长线于H,过点D作DF⊥BC于F,过点A作AN⊥BD,交BD的延长线于N,
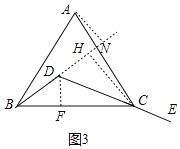
∵∠BDC=120°,
∴∠CDH=60°,
∵CH⊥BD,
∴∠DCH=30°,CD=6,
∴DH=3,CH=![]() DH=3
DH=3![]() ,
,
∵BH=![]() =
=![]() =5,
=5,
∴BD=BH﹣DH=2,
∵S△BDC=![]() BD×CH=
BD×CH=![]() ×BC×DF,
×BC×DF,
∴2×3![]() =2
=2![]() ×DF,
×DF,
∴DF=![]() ,
,
∵∠BDC=120°,
∴∠DBC+∠DCB=60°,
又∵∠ABD+∠DBC=60°,
∴∠ABD=∠DCB,
∴sin∠ABD=sin∠DCB=![]() ,
,
∴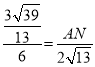 ,
,
∴AN=![]() ,
,
综上所述:点A到直线BD的距离为4![]() 或
或![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和点C,与y轴交于点B,
和点C,与y轴交于点B,![]() 的面积是6.
的面积是6.
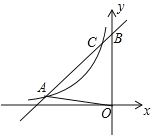
(1)求一次函数与反比例函数的表达式;(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,培养学生自主、团结协作能力,某校推出了以下四个项目供学生选择:A.家乡导游:B.艺术畅游:C.体育世界:D.博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目,学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息,解答下列问题:
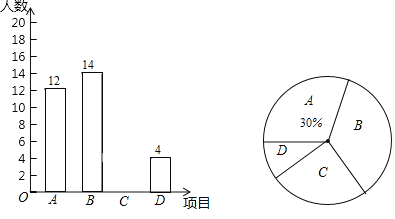
(1)求该班学生总人数;
(2)计算B项目所在扇形的圆心角的度数;
(3)将条形统计图补充完整;
(4)该校有1200名学生,请你估计选择“博物旅行”项目学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CO是AB边上的中线,∠AOC=60°,AB=2,点P是直线OC上的一个动点,则当△PAB为直角三角形时,边AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是坐标原点,点
是坐标原点,点![]() 是反比例函数
是反比例函数![]()
![]() 图像上一点,点
图像上一点,点![]() 在
在![]() 轴上,
轴上,![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() 交反比例函数
交反比例函数![]()
![]() 图像于点
图像于点![]() .
.
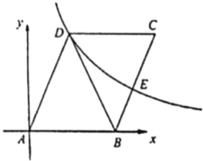
(1)平行四边形![]() 的面积等于______;
的面积等于______;
(2)设![]() 点横坐标为
点横坐标为![]() ,试用
,试用![]() 表示点
表示点![]() 的坐标;(要有推理和计算过程)
的坐标;(要有推理和计算过程)
(3)求![]() 的值;
的值;
(4)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道组织志愿者活动,选派志愿者到小区服务.若每一个小区安排4人,那么还剩下78人;若每个小区安排8人,那么最后一个小区不足8人,但不少于4人.求这个街道共选派了多少名志愿者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:①![]() ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com