
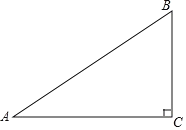
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
【答案】![]() 或7
或7![]()
【解析】分析:分两种情况:①如图1,作辅助线,构建矩形,先由勾股定理求斜边AB=10,由中点的定义求出AD和BD的长,证明四边形HFGB是矩形,根据同角的三角函数列式可以求DG和DF的长,并由翻折的性质得:∠![]() =∠A,
=∠A, ![]() =AD=5,由矩形性质和勾股定理可以得出结论:
=AD=5,由矩形性质和勾股定理可以得出结论: ![]() =
=![]() ;②如图2,作辅助线,构建矩形
;②如图2,作辅助线,构建矩形![]() ,同理可以求出
,同理可以求出![]() 的长.
的长.
详解:分两种情况:
如图1,过D作DG⊥BC与G,交A′E与F,过B作BH⊥A′E与H,
∵D为AB的中点,
∴BD=![]() AB=AD,
AB=AD,
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC=![]() ,
,
∴![]() ,
,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A=![]() ,
,
∴![]() ,
,
∴DF=3,
∴FG=43=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90,
∴四边形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=81=7,
∴A′H=A′EEH=76=1,
在Rt△AHB中,由勾股定理得:A′B=![]() ;
;

②如图2,过D作MN∥AC,交BC与于N,过A′作A′F∥AC,交BC的延长线于F,延长A′E交直线DN于M,
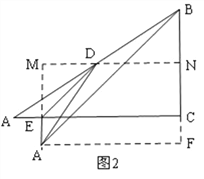
∵A′E⊥AC,
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四边形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B=![]() ;
;
综上所述![]() 的长为
的长为![]() 或
或![]()
故答案为: ![]() 或
或![]() .
.
本题考查的是图形的翻折变换及等腰直角三角形的性质、矩形的性质、平行线分线段成比例定理及勾股定理的综合运用,题型难度较大.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
5个主题进行了抽样调查(每位同学只选取最关注的一个),根据调查结果绘制了两幅不完
整的统计图,根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)在扇形统计图中“进取”部分扇形的圆心角是 度;
(4)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“感恩”的人数.
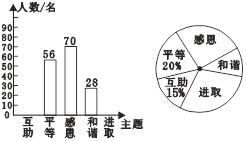
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
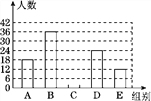
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
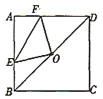
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,七(1)班的小明等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话,试根据对话中的信息,解答下列问题:
儿子:爸爸,成人门票是每张20元;学生门票是五折优惠;
团体票(16人及16人以上),按成人票的六折优惠.
爸爸:我们成人、学生一共12人,共需200元.
(1)设小明他们一共去了学生![]() 人,则成人购买门票的总费用为: 元;(用含
人,则成人购买门票的总费用为: 元;(用含![]() 的代数式表示)
的代数式表示)
(2)七(1)班小明他们一共去了几个成人、几个学生?
(3)正在购票时,小明发现七(2)班的小军等10名同学和他们的7名家长共17人也来购票,他们准备联合一起购买门票,请你为这29人的团队设计出最省的购票方案(直接写出方案即可,无需讨论),并求出此时的购票费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com