
 ,90°是45°的两倍,但三角函数值却是
,90°是45°的两倍,但三角函数值却是 倍;
倍; ,
,



 ,sin60°=
,sin60°= ,60°是30°的两倍,但三角函数值却是
,60°是30°的两倍,但三角函数值却是 倍;
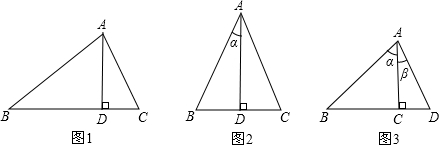
倍; AB•ACsin2α,S△ABD=
AB•ACsin2α,S△ABD= AB•ADsinα,
AB•ADsinα, AB•ACsin2α=2×
AB•ACsin2α=2× AB•ADsinα,
AB•ADsinα, ,
, =cosα,
=cosα, AB•ADsin(α+β),S△ABC=
AB•ADsin(α+β),S△ABC= AB•ACsinα,S△ACD=
AB•ACsinα,S△ACD= AC•ADsinβ,
AC•ADsinβ, AB•ADsin(α+β)=
AB•ADsin(α+β)= AB•ACsinα+
AB•ACsinα+ AC•ADsinβ,
AC•ADsinβ, +sinβ×
+sinβ× ,
, =cosβ,
=cosβ, =cosα,
=cosα, ×
× +
+ ×
× =
= .
.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2008-2009学年九年级(上)数学月考试卷(二)(英才班)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年浙江省衢州市华茂外国语学校中考数学二模试卷(解析版) 题型:解答题
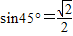 ,90°是45°的两倍,但三角函数值却是
,90°是45°的两倍,但三角函数值却是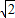 倍;
倍;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com