
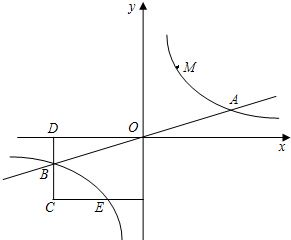
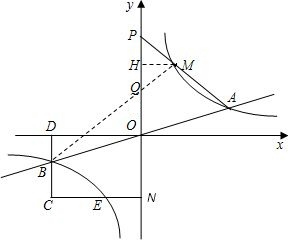
 如图,已知双曲线
如图,已知双曲线 与直线
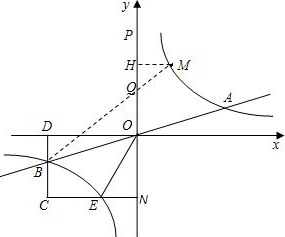
与直线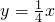 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C. x,
x, 得:
得: ,
,
 代入直线y=
代入直线y= x,得B点横坐标为-2n,
x,得B点横坐标为-2n, ),C点坐标(-2n,-n).--
),C点坐标(-2n,-n).-- )=n2.
)=n2. n2-
n2- n2,
n2,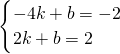 ,
,
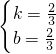 .
. x+
x+ .--
.-- 与直线y=
与直线y= x联立,
x联立,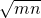 ,
,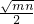 ),B点坐标(-2
),B点坐标(-2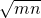 ,-
,-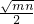 ),
),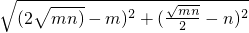 ,
,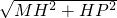 ,
,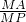 =
=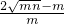 ,--
,--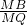 =
=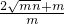 ,--
,--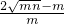 -
-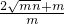 =-2.--
=-2.-- x,即可求出点B的坐标;再根据A点与B点关于原点对称,求出A点坐标;
x,即可求出点B的坐标;再根据A点与B点关于原点对称,求出A点坐标; ,即为-
,即为- ,又B点在直线y=
,又B点在直线y= x上,把y=-
x上,把y=- 代入直线y=
代入直线y= x,得B点横坐标为-2n,从而可用含n的代数式表示k及E点的坐标,然后根据四边形OBCE的面积=矩形ODCN面积-直角三角形ODB的面积-直角三角形ONE的面积,列出关于n的方程,解方程求出n的值,即可得出C、M两点的坐标,最后运用待定系数法求出直线CM的解析式;
x,得B点横坐标为-2n,从而可用含n的代数式表示k及E点的坐标,然后根据四边形OBCE的面积=矩形ODCN面积-直角三角形ODB的面积-直角三角形ONE的面积,列出关于n的方程,解方程求出n的值,即可得出C、M两点的坐标,最后运用待定系数法求出直线CM的解析式; 上,得出k=mn,再联立双曲线y=
上,得出k=mn,再联立双曲线y= 与直线y=
与直线y= x,求出A、B两点的坐标,由MA=pMP,MB=qMQ求出p、q,从而得出p-q的值.
x,求出A、B两点的坐标,由MA=pMP,MB=qMQ求出p、q,从而得出p-q的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 探索函数y=x+
探索函数y=x+| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直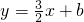 与双曲线
与双曲线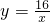 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.查看答案和解析>>
科目:初中数学 来源:2010年西藏中考数学模拟试卷(二)(解析版) 题型:解答题
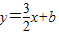 与双曲线
与双曲线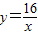 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com