解:(1)①∵△ABC、△ADE是等边三角形,
∴∠ACD=∠B=∠BAC=60°,∠ADE=60°,AD=DE,AC=BC=AB,
∵BD=AF,
∴CD=BF,
∵在△ACD和△CBF中,
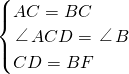
,
∴△ACD≌△CBF(SAS),
②判断四边形CDEF的形状是平行四边形,理由是:
∵△ACD≌△CBF,
∴∠BCF=∠DAC,AD=CF,
∵AD=DE,
∴DE=CF,
∵∠ACD=∠ADE=60°,∠ADB=∠ADE+∠BDE=∠ACD+∠DAC,
∴60°+∠DAC=60°+∠BDE,
∴∠DAC=∠BDE,
∵∠BCF=∠DAC,
∴∠BDE=∠BCF,
∴DE∥CF,
∵DE=CF,
∴四边形CDEF的形状是平行四边形;
(2)四边形CDEF的形状是平行四边形,
理由是:∵∠ACB=∠ABC=60°,
∴∠ACD=∠FBC=120°,
∵BD=AF,BC=AB,
∴CD=BF,
∵在△FBC和△DCA中,

,
∴△FBC≌△DCA(SAS),
∴∠DAC=∠BCF,FC=AD,
∵AD=DE,
∴FC=DE,
∵∠ACB=60°=∠DAC+∠ADC=∠BCF+∠ADC,
∠ADE=60°=∠ADC+∠CDE,
∴∠BCF=∠EDC,
∴CF∥DE,
∵FC=DE,
∴四边形CDEF是平行四边形;
(3)点D在边BC的中点上时,∠DEF=30°,
理由是:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵点D在边BC的中点上,
∴∠DAC=

∠BAC=30°,
∴∠BCF=∠DAC=30°,
∵四边形CDEF是平行四边形,
∴∠DEF=∠DCF=30°,
即点D在边BC的中点上时,∠DEF=30°.
分析:(1)①根据等边三角形的性质推出∠ACD=∠B=∠BAC=60°,∠ADE=60°,AD=DE,AC=BC=AB,求出CD=BF,根据SAS证出△ACD≌△CBF即可;②根据全等三角形的性质得出∠BCF=∠DAC,AD=CF,求出DE=CF,求出∠BDE=∠BCF,推出DE∥CF,根据平行四边形的判定推出即可;
(2)求出∠ACD=∠FBC=120°,CD=BF,根据SAS证出△FBC≌△DCA,推出∠DAC=∠BCF,FC=AD,求出FC=DE,求出∠BCF=∠EDC,推出CF∥DE,根据平行四边形的判定推出即可;
(3)点D在边BC的中点上时,∠DEF=30°,根据等腰三角形的性质得出∠DAC=

∠BAC=30°,推出∠BCF=∠DAC=30°,∠DEF=∠DCF=30°,即可得出答案.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质,等腰三角形的性质等知识点的应用,主要考查学生的推理能力,题目比较典型,证明过程类似.

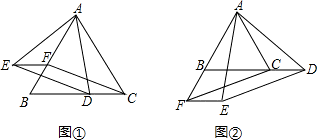 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.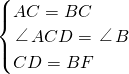 ,
, ,
, ∠BAC=30°,
∠BAC=30°, ∠BAC=30°,推出∠BCF=∠DAC=30°,∠DEF=∠DCF=30°,即可得出答案.
∠BAC=30°,推出∠BCF=∠DAC=30°,∠DEF=∠DCF=30°,即可得出答案.

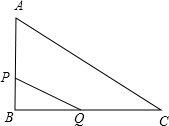
 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.