
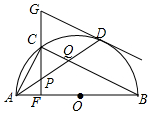
 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )| A. | ①②④ | B. | ②③⑤ | C. | ③④ | D. | ②⑤ |
分析 由于$\widehat{AC}$与$\widehat{BD}$不一定相等,根据圆周角定理可知①错误;
由于$\widehat{AC}$与$\widehat{BD}$不一定相等,那么$\widehat{AD}$与$\widehat{BC}$也不一定相等,根据圆心角、弧、弦的关系定理可知②错误;
先由垂径定理得到A为$\widehat{CE}$的中点,再由C为$\widehat{AD}$的中点,得到$\widehat{CD}$=$\widehat{AE}$,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可知③正确;
连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,可知④正确;
由于$\widehat{AC}$与$\widehat{BD}$不一定相等,而由垂径定理可得出$\widehat{BC}$=$\widehat{BE}$,则$\widehat{AD}$与$\widehat{BE}$不一定相等,∠GDA与∠BCE不一定相等,又∠BCE即∠PCQ=∠PQC,所以∠GDA与∠PQC不一定相等,可知⑤错误.
解答 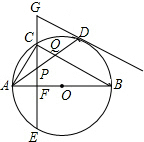 解:∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
解:∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
∴$\widehat{AC}$=$\widehat{CD}$≠$\widehat{BD}$,
∴∠BAD≠∠ABC,故①错误;
∵$\widehat{AC}$≠$\widehat{BD}$,
∴$\widehat{AC}$+$\widehat{CD}$≠$\widehat{BD}$+$\widehat{CD}$,
即$\widehat{AD}$≠$\widehat{BC}$,
∴AD≠BC,故②错误;
∵弦CE⊥AB于点F,
∴A为$\widehat{CE}$的中点,即$\widehat{AE}$=$\widehat{AC}$,
又∵C为$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴$\widehat{AE}$=$\widehat{CD}$,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为圆O的直径,
∴∠ACQ=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
连接OD,
则OD⊥GD,∠OAD=∠ODA,
∵∠ODA+∠GDP=90°,∠EPA+∠FAP=∠FAP+∠GPD=90°,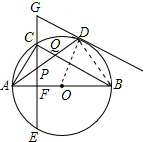
∴∠GPD=∠GDP;
∴GP=GD,故④正确;
∵CE⊥AB,
∴$\widehat{BC}$=$\widehat{BE}$,
∵$\widehat{AD}$≠$\widehat{BC}$,
∴$\widehat{AD}$≠$\widehat{BE}$,
∴∠GDA≠∠BCE,
又∵∠BCE=∠PQC,
∴∠GDA≠∠PQC,
∴CB与GD不平行,故⑤错误.
综上可知,正确的结论是③④,一共2个.
故选:C.
点评 此题是圆的综合题,其中涉及到切线的性质,圆周角定理,垂径定理,圆心角、弧、弦的关系定理,相似三角形的判定与性质,以及三角形的外接圆与圆心,平行线的判定,熟练掌握性质及定理是解决本题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
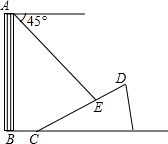 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
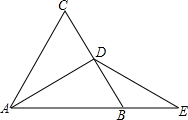 如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.
如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
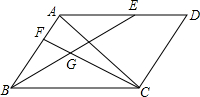 如图,平行四边形ABCD中,AB=5,AD=7,AB⊥AC,点E在边AD上,满足$\frac{AE}{AD}$=$\frac{2}{3}$,点F在AB上,满足$\frac{AF}{AB}$=$\frac{2}{5}$,连结BE和CF相交于点G,则线段CG的长度是$\frac{10\sqrt{7}}{7}$.
如图,平行四边形ABCD中,AB=5,AD=7,AB⊥AC,点E在边AD上,满足$\frac{AE}{AD}$=$\frac{2}{3}$,点F在AB上,满足$\frac{AF}{AB}$=$\frac{2}{5}$,连结BE和CF相交于点G,则线段CG的长度是$\frac{10\sqrt{7}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
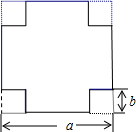 如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?
如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com