
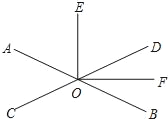
【题目】如图,直线AB与CD相交于点O,∠AOC=50°,OE平分∠AOD,OF平分∠BOD.
(1)填空:∠BOD= 度;
(2)试说明OE⊥OF.
【答案】(1)50;(2)先根据平角的定义求得∠AOD的度数,再根据角平分线的性质求得∠EOD、∠DOF的度数,从而得到结果.
【解析】
试题(1)根据对角线相等即可得到结果;
(2)先根据平角的定义求得∠AOD的度数,再根据角平分线的性质求得∠EOD、∠DOF的度数,从而得到结果.
(1)由图可得∠BOD=∠AOC=50°;
(2)∵∠AOC=50°,
∴∠AOD=180°-∠AOC =180°-50°=130°,
∵OE平分∠AOD,OF平分∠BOD
∴∠EOD=![]() ∠AOD=
∠AOD=![]() =65°,∠DOF=
=65°,∠DOF=![]() ∠BOD=
∠BOD=![]() =25°,
=25°,
∴∠EOF=∠EOD+∠DOF=65°+25°=90°,
∴OE⊥OF.


科目:初中数学 来源: 题型:
【题目】一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则用来表示y与x之间关系的选项是( ) 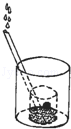
A.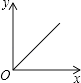
B.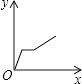
C.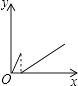
D.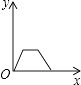
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=![]() ∠BOD,∠COE=72°,则∠EOB=( )
∠BOD,∠COE=72°,则∠EOB=( )
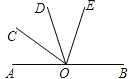
A. 36° B. 72°
C. 108° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD、CEFG均为正方形. 
(1)求证:BE=DG.
(2)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明. 
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC和BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB,若FB=1,AF=![]() ,则BD=_____.
,则BD=_____.
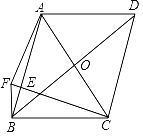
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B表示的数分别是a、b,点A在0和1对应的两点(不包括这两点)之间移动,点B在﹣3,﹣2对应的两点之间移动,下列四个代数式的值可能比2018大的是( )
![]()
A. ![]() B. b﹣a C. (a﹣b)2 D.
B. b﹣a C. (a﹣b)2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com