
【题目】四边形ABCD是边长为4的正方形,点P是平面内一点.且满足BP⊥PC,现将点P绕点D顺时针旋转90度,则CQ的最大值=_____.

【答案】2+2![]() .
.
【解析】
如图: 由BP⊥CP可知点P在以BC中点O为圆心,2为半径的圆上,⊙O绕点D旋转90°后为⊙O′,则P点旋转90°后的对应点Q在⊙O′上,所以CO′的延长线与⊙O′的交点是CQ的最大值,过O′作O′E⊥CD延长线于E,通过证明△DEO′≌△DOC可求出DE、EO′的长,根据勾股定理求出CO′的长,进而求出CQ的长即可.
如图:⊙O旋转90°得⊙O′,连接CO′交⊙O′于Q,则CQ即为所求,过O′作O′E⊥CD延长线于E,
∵BP⊥CP,
∴P点在在以BC中点O为圆心,2为半径的圆上,
∵⊙O′是⊙O旋转90°所得,
∴OD=O′D,
在△DEO′和△CDO中,∠DEO′=∠OCD=90°,∠DO′E=∠ODC,OD=O′D,
∴△DEO′≌△DOC,
∴DE=OC=2,EO′=CD=4,CE=6,
∴CO′=![]() =
=![]() ,
,
∴CQ=2+![]() .
.
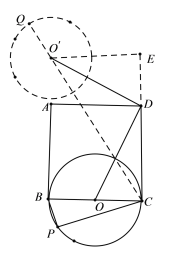
故答案为:2+![]()


科目:初中数学 来源: 题型:
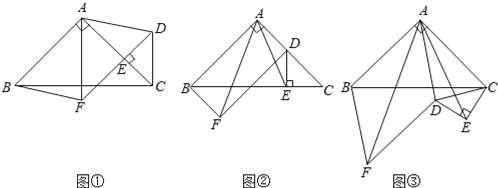
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
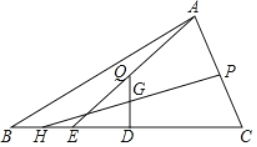
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
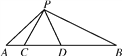
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )

A. 20![]() 米 B. (20
米 B. (20![]() -8)米 C. (20
-8)米 C. (20![]() -28)米 D. (20
-28)米 D. (20![]() -20)米
-20)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com