
 如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离.
如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离.科目:初中数学 来源: 题型:
 23、如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离.
23、如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是( )
如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是( )查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省建水三合中学八年级上学期期中考试数学试卷(带解析) 题型:解答题
(本题满分6分)如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,求从B到灯塔C的距离。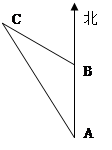
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省建水县建民中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,求从B到灯塔C的距离。
查看答案和解析>>
科目:初中数学 来源:2014届云南省八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,求从B到灯塔C的距离。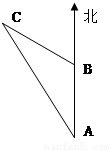
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com