
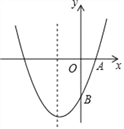
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
【答案】(1) y=x2+2x﹣3;(2) 存在,理由见解析.
【解析】试题分析:(1)利用待定系数法即可求得函数的解析式;
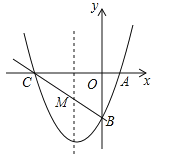
(2)抛物线与x轴的除A外的另一个交点C就是A的对称点,则BC与对称轴的交点就是M,首先求得C的坐标,然后求得BC的解析式,进而求得M的坐标.
试题解析:解:(1)根据题意得: 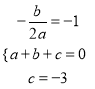 ,解得:
,解得:  ,则二次函数的解析式是y=x2+2x﹣3;
,则二次函数的解析式是y=x2+2x﹣3;
(2)存在.设抛物线与x轴的另一个交点是C,由抛物线的对称性得BC与对称轴的交点就是M.∵C点的坐标是(﹣3,0),设直线BC的解析式是y=kx﹣3,则0=﹣3k﹣3,解得k=﹣1,∴直线BC的解析式是y=﹣x﹣3.
当x=﹣1时,y=﹣2,∴点M的坐标是(﹣1,﹣2).


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CD⊥AB于点D,DA=DC=4,DB=2,AF⊥BC于点F,交DC于点E.
(1)求线段AE的长;
(2)若点G是AC的中点,点M是线段CD上一动点,连结GM,过点G作GN⊥GM交直线AB于点N,记△CGM的面积为S1,△AGN的面积为S2.在点M的运动过程中,试探究:S1与S2的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
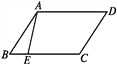
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式配成完全平方式:
①x2+6x+______=(x+____)2 ②x2-5x+_____=(x-____)2;
③x2+ x+______=(x+____)2 ④x2-9x+_____=(x-____)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com