
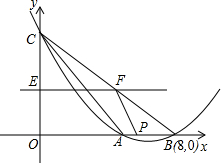
 ��ͼ��������y=ax2+bx+c��a��0����x����A��B���㣬��y����C�㣬A����B�����࣬��֪B�������ǣ�8��0����tan��ABC=$\frac{1}{2}$����ABC�����Ϊ8��
��ͼ��������y=ax2+bx+c��a��0����x����A��B���㣬��y����C�㣬A����B�����࣬��֪B�������ǣ�8��0����tan��ABC=$\frac{1}{2}$����ABC�����Ϊ8������ ��1�����A��B��C��������������������y=ax2+bx+c������ý⣮
��2���������������εõ�$\frac{EF}{OB}=\frac{CE}{CO}$����t�Ĺ�ϵʽ����ý⣮
��3����Ϊ��P��B��F����Rt�����ֱ�������������t��ֵ��
��� �⣺��1��������֪��COB=90��B��8��0��OB=8��
��Rt��OBC��tan��ABC=$\frac{OC}{OB}=\frac{1}{2}$OC=OB��tan��ABC=8��$\frac{1}{2}$=4��
��C��0��4����${S}_{��ABC}=\frac{1}{2}AB•OC=8$��
��AB=4��
��A��4��0��
��A��B��C������������y=ax2+bx+c��a��0����$\left\{\begin{array}{l}{16a+4b+c=0}\\{64a+8b+c=0}\\{c=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{1}{8}}\\{b=-\frac{3}{2}}\\{c=4}\end{array}\right.$��
���������ߵĽ���ʽΪ$y=\frac{1}{8}{x}^{2}-\frac{3}{2}x+4$��
��2��������ã�0��t��4��
CE=t��BP=2t��OP=8-2t��
��EF��x�ᣬ
���CEF�ס�COB��
��$\frac{EF}{OB}=\frac{CE}{CO}$��EF=2t��
��$\begin{array}{l}\frac{1}{EF}+\frac{1}{OP}=\frac{1}{2t}+\frac{1}{8-2t}\\=\frac{8}{2t��8-2t��}=\frac{2}{t��4-t��}\end{array}$��
Ҫʹ$\frac{1}{EF}+\frac{1}{OP}$��ֵ��С����t��4-t��Ҫ�����
�൱t=2ʱ��$\frac{1}{EF}+\frac{1}{OP}$��СֵΪ$\frac{1}{2}$��
��3����ʹ�õ�P��B��F����Rt����
�ɵá�FPB=90�㣬���PFB=90�㣬
��t��2��ֵ��
�ʴ�Ϊ��2��
����FPB=90�㣬��P��B��F����Rt��ʱ����ʱ$\frac{FP}{BP}=\frac{1}{2}=\frac{4-t}{2t}$����ã�t=2��
����PFB=90�㣬��P��B��F����Rt��ʱ����ã�t=$\frac{20}{9}$��
���� ���⿼����һ��ʽ����κ����Ľ���ʽ�����κ����뷽�̡�����֪ʶ���ۺ�Ӧ�ã�������֪ʶ�뷽�̡�����֪ʶ�л��ؽ����һ����������һ���ѶȽϴ���������ؼ������ڽ���������ת��Ϊ�������⣬�������ü���ͼ�ε��й����ʡ������Ͷ��κ�����֪ʶ����ע���ھ���Ŀ�е�һЩ�������������ֵ���ѧ˼���Ƿ�������˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
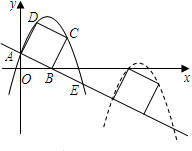 ��ͼ����ֱ֪��y=-2x+2����������A��B���㣬���߶�ABΪ������������ABCD��AB��AD=1��2������A��D��C����������ֱ����һ������ΪE��
��ͼ����ֱ֪��y=-2x+2����������A��B���㣬���߶�ABΪ������������ABCD��AB��AD=1��2������A��D��C����������ֱ����һ������ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
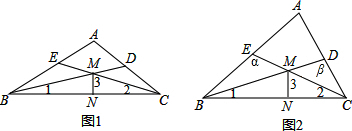
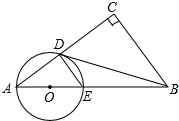 ��֪����ͼ����Rt��ABC�У���C=90�㣬��O��AB�ϣ���OΪԲ�ģ�OA��Ϊ�뾶��Բ��AC��AB�ֱ��ڵ�D��E������DE��DB������CBD=��A��
��֪����ͼ����Rt��ABC�У���C=90�㣬��O��AB�ϣ���OΪԲ�ģ�OA��Ϊ�뾶��Բ��AC��AB�ֱ��ڵ�D��E������DE��DB������CBD=��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
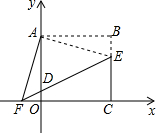 ��ͼ����ƽ��ֱ������ϵ�У�������OABC�ĵ�A��y���ϣ���C��x���ϣ���B��4��4������E��BC���ϣ�����ABE�Ƶ�A˳ʱ����ת90�㣬�á�AOF������EF��y���ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У�������OABC�ĵ�A��y���ϣ���C��x���ϣ���B��4��4������E��BC���ϣ�����ABE�Ƶ�A˳ʱ����ת90�㣬�á�AOF������EF��y���ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
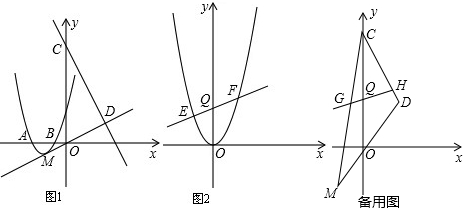
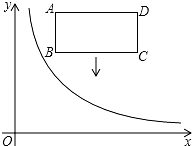 ��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ��;���ABCD�ڵ�һ���ޣ�ADƽ����x�ᣬ��AB=2��AD=4����A������Ϊ��2��6����������ABCD����ƽ�ƣ�ƽ�ƺ�ľ��μ�ΪA��B��C��D����ƽ�ƹ����У�����������ǡ�����ڷ���������ͼ���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ��;���ABCD�ڵ�һ���ޣ�ADƽ����x�ᣬ��AB=2��AD=4����A������Ϊ��2��6����������ABCD����ƽ�ƣ�ƽ�ƺ�ľ��μ�ΪA��B��C��D����ƽ�ƹ����У�����������ǡ�����ڷ���������ͼ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com