
 +1)s时,E点到达P点的位置,一开口向下的抛物线y=
+1)s时,E点到达P点的位置,一开口向下的抛物线y=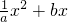 ,过P、O两点且与射线AD相交于点H,与x轴相交于点Q(异于原点).请问a是否存在取某一值或某一范围,使OQ+PH的值为定值?如果存在,求出a值或a的取值范围;如果不存在,请说明理由.
,过P、O两点且与射线AD相交于点H,与x轴相交于点Q(异于原点).请问a是否存在取某一值或某一范围,使OQ+PH的值为定值?如果存在,求出a值或a的取值范围;如果不存在,请说明理由.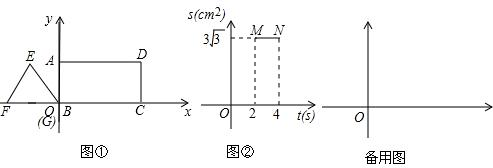
 cm2;
cm2; x•
x• x=3
x=3 ,解得 x=2
,解得 x=2 (cm);
(cm);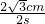 =
= m/s;
m/s; cm,它的移动速度为
cm,它的移动速度为 m/s.
m/s.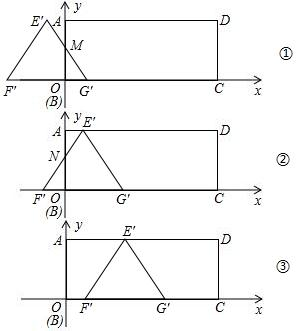 (2)当点E运动到y轴上时,t=1s;当点F运动到y轴上时,t=2s;
(2)当点E运动到y轴上时,t=1s;当点F运动到y轴上时,t=2s;
 t•(
t•( ×
× t)=
t)= t2;
t2; •(2
•(2 -
- t)•
t)• (2
(2 -
- t)=
t)= (2-t)2,
(2-t)2, ×2
×2 ×(
×( ×2
×2 )-
)- (2-t)2=3
(2-t)2=3 -
- (2-t)2;
(2-t)2; ×2
×2 ×(
×( ×2
×2 )=3
)=3 ;
;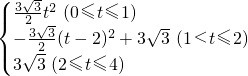 ,图象如下:
,图象如下: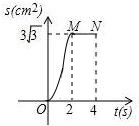
 +1)秒,速度为每秒
+1)秒,速度为每秒 cm,
cm, (
( +1)=3+
+1)=3+ ,
, -
- =3,
=3,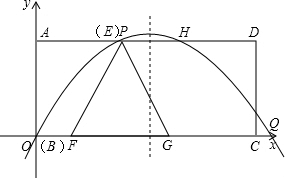
 x2+bx的对称轴为直线x=-
x2+bx的对称轴为直线x=-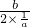 =-
=-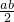 ,
,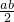 对称,
对称,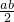 -3)=-ab-6=-(a-3)-6=-a+3-6=-a-3,
-3)=-ab-6=-(a-3)-6=-a+3-6=-a-3,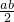 )-a-3=-(a-3)-a-3=-a+3-a-3=-2a,
)-a-3=-(a-3)-a-3=-a+3-a-3=-2a,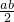 )=ab+6,
)=ab+6,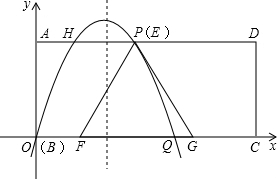
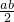 )+(-a-3)=-ab+ab+6=6,
)+(-a-3)=-ab+ab+6=6,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com