
 ��ͼ����A��C�ֱ���һ�κ���y=-$\frac{3}{4}$x+3��ͼ����y�ᡢx��Ľ��㣬��B���C����ԭ��Գƣ����κ���y=$\frac{1}{8}$x2+bx+c��ͼ����B���Ҹö��κ���ͼ���ϴ���һ��D��ʹ�ı���ABCD�ܹ���ƽ���ı��Σ�
��ͼ����A��C�ֱ���һ�κ���y=-$\frac{3}{4}$x+3��ͼ����y�ᡢx��Ľ��㣬��B���C����ԭ��Գƣ����κ���y=$\frac{1}{8}$x2+bx+c��ͼ����B���Ҹö��κ���ͼ���ϴ���һ��D��ʹ�ı���ABCD�ܹ���ƽ���ı��Σ����� ��1��������һ�κ����Ľ���ʽȷ��A���C�����꣬�����õ�B���C����ԭ��ԳƵõ���B�������BC�ij�����������ƽ���ı��ε��������D�����꣬Ȼ��ѵ�B�͵�D�����������κ���y=$\frac{1}{8}$x2+bx+c�ù���b��c�ķ����飬�ٽⷽ�������b��c���ɵõ����κ�������ʽ��
��2���������ù��ɶ��������AC=5��������t��ʾ��AP=t��CQ=t��AQ=5-t����PQ��ACʱ��֤����APQ�ס�CAO�����������Ʊȵõ�$\frac{t}{5}$=$\frac{5-t}{4}$�����t=$\frac{25}{9}$��Ȼ��ⷽ�����t���ɣ�
����QH��AD��H����ͼ����֤����AQH�ס�CAO���������Ʊȿɱ�ʾ��QH=$\frac{3}{5}$��5-t�����ٸ��������������ʽ������S�ı���PDCQ=S��ACD-S��AQP�õ��ı���PDCQ�����=$\frac{3}{10}$t2-$\frac{3}{2}$t+12��Ȼ����ݶ��κ�����������⣮
��� �⣺��1����x=0��y=-$\frac{3}{4}$x+3=3�����A��0��3����
��y=0��-$\frac{3}{4}$x+3=0�����x=4�����C��4��0����
�ߵ�B���C����ԭ��Գƣ�
���B��-4��0����BC=8��
���ı���ABCD��ƽ���ı��Σ�
��AD��x�ᣬAD=BC=8��
��D��8��3����
����B��-4��0������D��8��3����������y=$\frac{1}{8}$x2+bx+c��$\left\{\begin{array}{l}{\frac{1}{8}��16-4b+c=0}\\{\frac{1}{8}��64+8b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-\frac{1}{4}}\\{c=-3}\end{array}\right.$��
����κ�������ʽy=$\frac{1}{8}$x2-$\frac{1}{4}$x-3��
��2���١�A��0��3����C��4��0����
��AC=$\sqrt{{3}^{2}+{4}^{2}}$=5��
������P�˶���t��ʱ����AP=t��CQ=t��AQ=5-t��
��AD��BC��
���PAQ=��OCA��
��PQ��AC��
���AQP=90�㣬
���APQ�ס�CAO��
��$\frac{AP}{AC}$=$\frac{AQ}{OC}$����$\frac{t}{5}$=$\frac{5-t}{4}$�����t=$\frac{25}{9}$��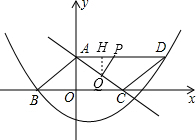
�൱t=$\frac{25}{9}$��ʱ��PQ��AC��
����QH��AD��H����ͼ��
�ߡ�HAQ=��OCA��
���AQH�ס�CAO��
��$\frac{AQ}{AC}$=$\frac{QH}{OA}$����$\frac{5-t}{5}$=$\frac{QH}{3}$�����QH=$\frac{3}{5}$��5-t����
��S�ı���PDCQ=S��ACD-S��AQP
=$\frac{1}{2}$•3•8-$\frac{1}{2}$•t•$\frac{3}{5}$��5-t��
=$\frac{3}{10}$t2-$\frac{3}{2}$t+12
=$\frac{3}{10}$��t-$\frac{5}{2}$��2+$\frac{81}{8}$��
�൱t=$\frac{5}{2}$ʱ���ı���PDCQ�������С����С���Ϊ$\frac{81}{8}$��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ��������ʺ�ƽ���ı��ε����ʣ������ô���ϵ����������κ�������ʽ������һ�κ�������κ���ͼ����������Ľ������ꣻ�ܹ������������Σ��������Ʊȱ�ʾ�߶�֮��Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
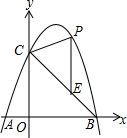 ��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=ax2+bx+c��ͼ����y�ύ�ڵ�C��0��8������x�ύ��A��B���㣬����A��-2��0����B��6��0����
��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=ax2+bx+c��ͼ����y�ύ�ڵ�C��0��8������x�ύ��A��B���㣬����A��-2��0����B��6��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
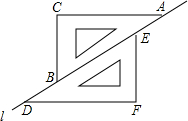 ��ͼ��������ȫ��ͬ�����dz�ABC��DEF��ֱ��l�ϻ�������������һ��������ʹ�ı���CBFEΪ���Σ�����ѡ���д�����ǣ�������
��ͼ��������ȫ��ͬ�����dz�ABC��DEF��ֱ��l�ϻ�������������һ��������ʹ�ı���CBFEΪ���Σ�����ѡ���д�����ǣ�������| A�� | BD=AE | B�� | CB=BF | C�� | BE��CF | D�� | BAƽ�֡�CBF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
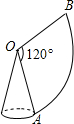 ��ͼ����һԲ�Ľ�Ϊ120�㣬�뾶��Ϊ6cm�����Σ�����OA��OB�غϺ�Χ��һԲ���棬��ôԲ�ĸ���4$\sqrt{2}$ cm��
��ͼ����һԲ�Ľ�Ϊ120�㣬�뾶��Ϊ6cm�����Σ�����OA��OB�غϺ�Χ��һԲ���棬��ôԲ�ĸ���4$\sqrt{2}$ cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y=$\frac{k}{x}$��x��0����ͼ��BC�ϵĵ�D��AB���ڵ�E������DE����E��AB���е㣮
��ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y=$\frac{k}{x}$��x��0����ͼ��BC�ϵĵ�D��AB���ڵ�E������DE����E��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com