
【题目】如图,AB∥CD,E 是直线 CD 上的一点,且 ∠BAE=30°, 是直线 CD 上的一动点,M是 AP 的中点,直线 MN⊥AP 且与 CD 交于点 N,设 ∠BAP=X°,∠MNE=Y°.

(1)在图2 中,当 x=12 时,∠MNE= ;在图 3 中,当 x=50 时,∠MNE= ;
(2)研究表明:y与x之间关系的图象如图4所示( 不存在时,用空心点表示),请你根据图象直接估计当 y=100 时,x= ;

(3)探究:当 x= 时,点 N 与点 E 重合;
(4)探究:当 x>105 时,求y与x之间的关系式.
【答案】(1)102°,40°;(2)10或170;(3)15或105.(4)y=270-x
【解析】(1)当x=12时,根据三角形外角的性质可:∠MNE=90°+12°=102°;
当x=50°,根据直角三角形两锐角互余可得结论;
(2)由图象直接得出结论;
(3)分两种情况:①P在E的左侧,②P在E的右侧,根据平行线的性质和中垂线的性质可得结论;
(4)如图7,根据三角形外角和为360°列式可得结论.
解:(1)如图2,∵AB∥CD,
∴∠BAP=∠APN=x°,
∵MN⊥AP,
∴∠PMN=90°,
∴∠MNE=∠PMN+∠APN=90°+x°,
当x=12时,∠MNE=(90+12)°=102°;
即y=102°,
如图3中,当x=50时,∠APN=50°,
∴y=∠MNE=90°-x°=90°-50°=40°,
故答案为:102°,40°;
(2)如图2,当0<x<30时,y=90+x,
此时,y=100时,90+x=100,x=10,
由图4可知:y=100时,还有x=170,
∴当y=100时,x=10或170,
故答案为:10或170;
(3)①P在E的左侧时,当N与E重合时,如图5,∠BAE=∠AEP=30°,
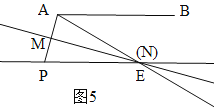
∵MN是AP的中垂线,
∴AE=PE,
∴∠AEM=∠PEM=15°,
∴∠EAP=90°-15°=75°,
∴∠BAP=x=30°+75°=105°,
②P在E的右侧时,当N与E重合时,如图6,
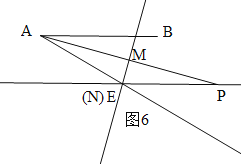
∵AB∥CD,
∴∠BAP=∠APE=x,
同理得:AE=PE,
∴∠EAM=∠EPM=x,
∵∠BAE=30°,
∴∠BAP=x=∠EAP=![]() ∠BAE=15°,
∠BAE=15°,
综上所述,当x=15或105时,点N与点E重合;
故答案为:15或105;
(4)当x>105时,如图7,
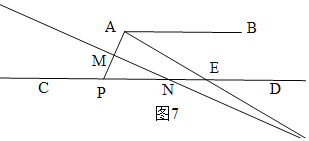
∵AB∥CD,
∴∠APC=∠BAP=x,
∵∠APC+∠MNE+∠AMN=360°,∠AMN=90°,
∴∠APC+∠MNE=360°-90°=270°,
∴∠MNE=270°-∠APC=270°-∠BAP,
即y=270-x.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒. 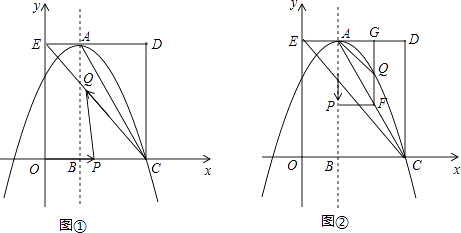
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y= ![]() (k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为
(k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为 ![]() ,点C横坐标为1.
,点C横坐标为1. 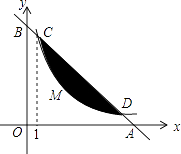
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+a﹣c=0,其中a、b、c分别为△ABC三边的长.下列关于这个方程的解和△ABC形状判断的结论错误的是( )
A. 如果x=﹣1是方程的根,则△ABC是等腰三角形
B. 如果方程有两个相等的实数根,则△ABC是直角三角形
C. 如果△ABC是等边三角形,方程的解是x=0或x=﹣1
D. 如果方程无实数解,则△ABC是锐角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.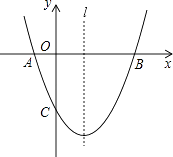
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.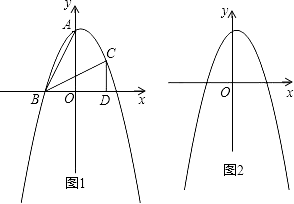
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
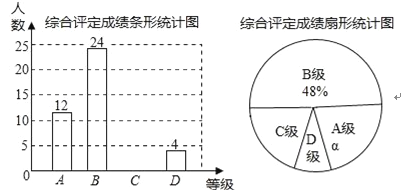
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com