
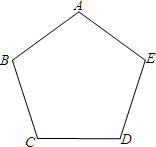
 如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
 =108°,AB=BC=CD=DE=AE,
=108°,AB=BC=CD=DE=AE, ×(180°-108°)=36°,
×(180°-108°)=36°,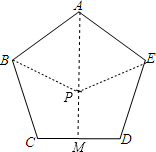
 ×(180°-54°)=63°,∠AEP=∠APE=63°,
×(180°-54°)=63°,∠AEP=∠APE=63°,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
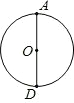
 19、如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
19、如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、甲、乙皆正确 | B、甲、乙皆错误 | C、甲正确、乙错误 | D、甲错误、乙正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:
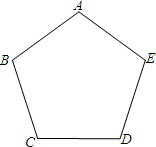 (2013•台湾)如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
(2013•台湾)如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:查看答案和解析>>
科目:初中数学 来源:2013年台湾省中考数学试卷(解析版) 题型:选择题
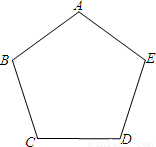
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com