
 已知数轴上有A,B,C三个点,如图所示,它们表示的数分别是-18,-6,14.
已知数轴上有A,B,C三个点,如图所示,它们表示的数分别是-18,-6,14.分析 (1)根据数轴上点的位置求出AB与BC的长即可;
(2)分五种情况考虑:①当0≤t≤12时,P动而Q未动,Q在A处;②当12<t<18时,P动Q动,且Q未超过P,Q在线段AP上;③当18≤t≤22$\frac{2}{3}$时,Q在线段PC上(Q未到达C点);④当22$\frac{2}{3}$<t<25时,Q在线段PC上(Q从C点返回);⑤当25≤t≤32时,Q在线段AP上,分别求出PQ即可.
解答 解:(1)∵A,B,C三个点表示的数分别是-18,-6,14,
∴AB=-6-(-18)=12,BC=14-(-6)=20.
故答案为12,20;
(2)①当0≤t≤12时,P动而Q未动,Q在A处,PQ=t;
②当12<t<18时,P动Q动,且Q未超过P,Q在线段AP上,
PQ=t-3(t-12)=36-2t;
③当18≤t≤22$\frac{2}{3}$时,Q在线段PC上(Q未到达C点),
PQ=3(t-12)-t=2t-36;
④当22$\frac{2}{3}$<t<25时,Q在线段PC上(Q从C点返回),
PQ=(12+20-22$\frac{2}{3}$)-4(t-22$\frac{2}{3}$)=100-4t;
⑤当25≤t≤32时,Q在线段AP上,
PQ=4(t-25)=4t-100.
点评 此题考查了整式的加减,数轴,以及两点间的距离,弄清题意正确分类是解本题的关键.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
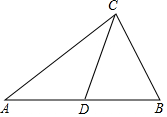 如图,已知CD是△ABC的边AB上的中线.
如图,已知CD是△ABC的边AB上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
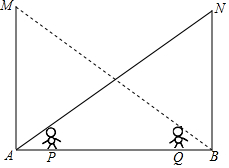 如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.
如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com