
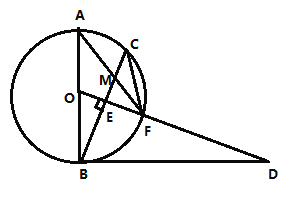
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)欲证明BD是⊙O的切线,只要证明BD⊥AB;
(2)连接AC,证明△FCM∽△FAC即可解决问题;
(3)连接BF,想办法求出BF,FM即可解决问题.
(1)∵![]() ,
,
∴∠AFC=∠ABC,
又∵∠AFC=∠ODB,
∴∠ABC=∠ODB,
∵OE⊥BC,
∴∠BED=90°,
∴∠ODB+∠EBD=90°,
∴∠ABC+∠EBD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)连接AC,

∵OF⊥BC,
∴![]() ,
,![]() ,
,
∴∠BCF=∠FAC,
又∵∠CFM=∠AFC,
∴△FCM∽△FAC,
∴![]() ;
;
(3)连接BF,
∵AB是⊙O的直径,且AB=10,
∴∠AFB=90°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划购买![]() ,
,![]() 两种型号的机器人加工零件.已知
两种型号的机器人加工零件.已知![]() 型机器人比
型机器人比![]() 型机器人每小时多加工
型机器人每小时多加工![]() 个零件,且
个零件,且![]() 型机器人加工
型机器人加工![]() 个零件用的时间与
个零件用的时间与![]() 型机器人加工
型机器人加工![]() 个零件所用的时间相同.
个零件所用的时间相同.
(1)求![]() ,
,![]() 两种型号的机器人每小时分别加工多少零件;
两种型号的机器人每小时分别加工多少零件;
(2)该工厂计划采购![]() ,
,![]() 两种型号的机器人共
两种型号的机器人共![]() 台,要求每小时加工零件不得少于
台,要求每小时加工零件不得少于![]() 个,则至少购进
个,则至少购进![]() 型机器人多少台?
型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
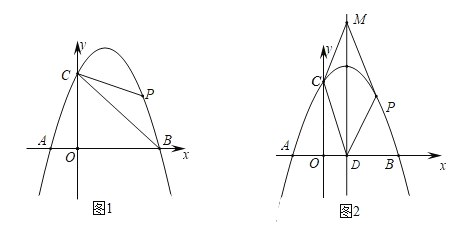
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线上在第一象限内的一个动点,且点
是抛物线上在第一象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的表达式;
(2)如图1,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数表达式,并求出当
的函数表达式,并求出当![]() 为何值时,
为何值时,![]() 的面积
的面积![]() 有最大值;
有最大值;
(3)如图2,设抛物线的对称轴为直线![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .在直线
.在直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
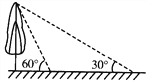
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
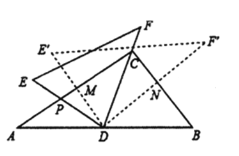
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.
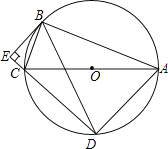
(1)求证:CB是∠ECA的角平分线;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年重庆国际马拉松赛于3月31日在南滨公园鸣枪开跑已知A、B两补给站之间的路程为1470米,志愿者甲、乙都从A站出发支援B站.甲先出发,且在途中停留了4分钟,甲出发6分钟后,乙才从A站出发.在整个行走过程中,两人保持各自速度匀速行走,两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达B站时,甲与B站相距的路程是_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()
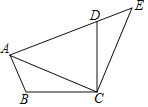
A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com